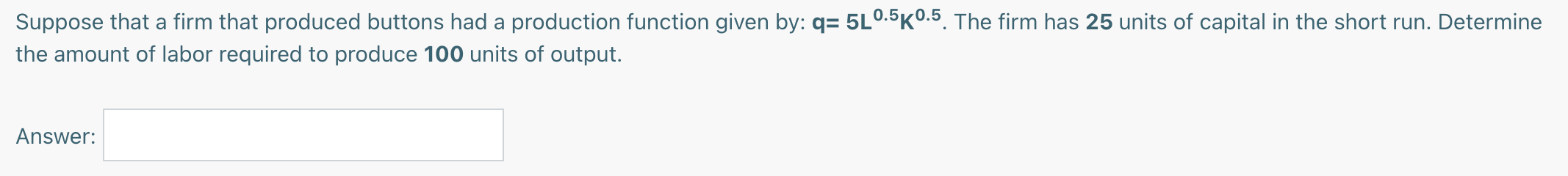Suppose the production function for a firm is given by: q=4L'5K'25. In the short run, the firm has 16 units of capital. Find the Marginal Product of Labor (MPL). Fill in the appropriate numbers in the function below. MPL : L'0'5 (Round to the nearest 2 decimal places if necessary.) Suppose that a firm has a production function given by: q: 10 L2 K. The firm has 10 units of capital in the short run. Which of the following will describe the marginal product of labor (MPL) for this production function? Select one: 0 a. Constant Marginal Returns to Labor 0 b. Increasing Marginal Returns to Labor 0 c. Decreasing Marginal Returns to Labor Suppose that a firm that produced buttons had a production function given by: q: 5L'5K'5. The firm has 25 units of capital in the short run. Determine the amount of labor required to produce 100 units of output. Answer: Consider the following production function: q: 4LK. Which term describe this production function's returns to scale? Select one: 0 a. Constant Returns to Scale 0 b. Increasing Returns to Scale 0 c. Decreasing Returns to Scale Suppose you own an acre of land. You could grow crops on that land. The cost of seeds is $100. The crops you grow from those seeds will sell for $250. You could also rent the land to another farmer. The rent you could earn is $300. Calculate your economic profit. (Do not include a $ sign in your answer.) Answer: Suppose the total cost function for a firm is given by: TC: 100 + 2q +4q2. Find the marginal cost function and then use that to determine the marginal cost of the 10th unit. (Do not include a $ Sign in your response.) Answer: Suppose the production function for a firm is given by: q=4L'75K'25. If the firm currently has 20 units of capital (K) and 10 units of labor (L), then calculate the Marginal Rate of Technical Substitution (MRTSLK). (Round to the nearest two decimal places if necessary.) Answer: Suppose the production function for a firm is given by: q=2L +4K. If the firm currently has 20 units of capital (K) and 10 units of labor (L), then calculate the Marginal Rate of Technical Substitution (M RTSLK). (Round to the nearest two decimal places if necessary.) Answer: Suppose that a firm had a production function given by: q=2L'5K'5. The rental rate for the firm is $10 and the wage is $5. Solve the optimization condition for K and then fill in the value that appears in front of L. K = L (Round to the nearest 2 decimal places if necessary.) Suppose that a firm had a production function given by: q=L'25K'75. The wage rate (w) is $5 and the rental rate (r) is $10. Calculate the amount of labor the firm would hire when it produces 400 units of output in a cost-minimizing way. (Round to the nearest 2 decimal places if necessary.)