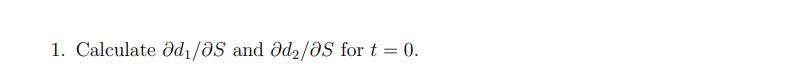
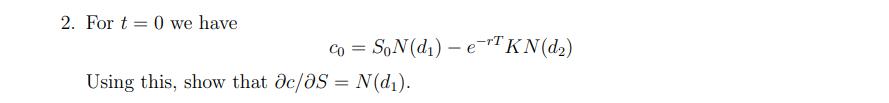
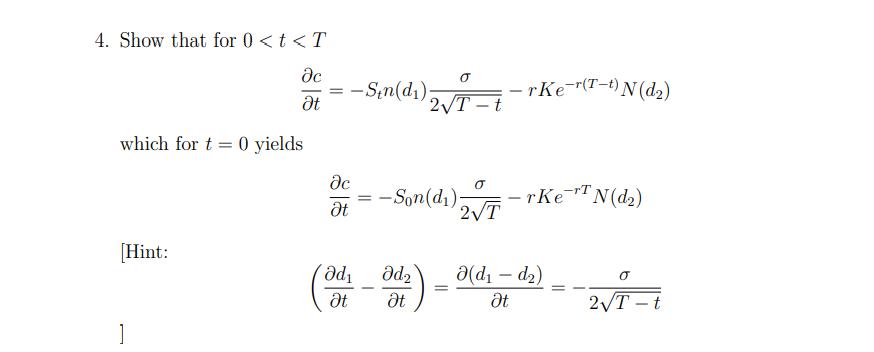
Suppose the time t price St of a non-dividend paying stock follows geometric Brownian motion, i.e., dS = Sidt + o Sdz = where is the expected return of the stock, o is the volatility of the stock, and dz with ~ N(0, 1). As we saw in class, under some additional assumptions (which you may assume are satisfied) any derivative written on this stock must satisfy the following differential equation: where where t is time, ft is the price of the derivative at time t, and r is the risk-free rate. This is the Black-Scholes differential equation. and af af as t In particular, a European style call option written on this stock must satisfy the Black- Scholes differential equation. The formula for the time 0 < t < T price of a European style call option with strike price K and expiration T is given by C = SN (d) - e-r(T-t) KN (d) d = +rSt + 1/05205 = Tft S2 In ( ) + (r + ) (T t) - oT-t Edt dd-oT-t 1 N(x) -1 +d= n(z)_dN (2) -dz, e = 2T dx 88 1 2 that is, N(x) and n(x) are the CDF and PDF, respectively, of a standard normal random variable. = In this exercise, you will verify that the formula for the price of a call option satisfies the Black-Scholes differential equation. In what follows, you may use the following fact (without proof): Sin(d) = e(Tt) Kn(d) 1. Calculate od/0S and ad/0S for t = 0. 2. For t=0 we have Co = SoN (d) - e-T KN (d) Using this, show that ac/0S = N(d). 3. Calculate c/as for t = 0. 4. Show that for 0 < t < T c t which for t= 0 yields [Hint: 1 = c t d t -Sin(d). = - O 2T-t - Son(d) 2T - d t rKer(T-t) N (d) -rKeN(d) (dd) t 2T-t 5. Show that the formula for the price of a European style call option satisfies the Black- Scholes differential equation. Do this for t = 0.