Suppose we are given an undirected graph G = (V, E). A Hamiltonian path in a graph G is a path that visits every vertex in V exactly once (i.e., the same vertex is never visited twice). If a graph G has n vertices, then a Hamiltonian path is a simple path consisting of n 1 edges.

Consider a complete graph on n vertices, which is typically denoted by Kn. In a complete graph, every pair of vertices is connected by an edge. In a complete graph, any ordering of the n vertices v1, . . . , vn gives us a Hamiltonian path. In particular, we have the sequence of n 1 edges:

(v1, v2),(v2, v3), . . . ,(vn1, vn)

There are n! possible ways to order n vertices, so there are n! Hamiltonian paths in a complete graph Kn

We can also ask how many Hamiltonian paths there are in Kn when we start at a vertex s and end at a vertex t. In this case, any ordering where we fix the first and last element corresponds to a Hamiltonian path, leading to (n 2)! different Hamiltonian paths starting at vertex s and ending at vertex t.

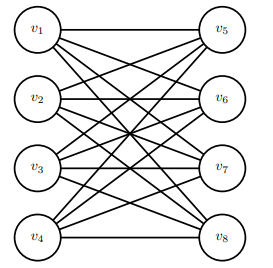
Consider a complete bipartite graph whose vertices are partitioned into two subsets: V1 of size m and V2 of size n. Typically, we denote such a complete bipartite graph by Km,n. In a complete bipartite graph, every node in V1 is connected by an edge to every node in V2 (with no edges between nodes in the same partition). The following graph depicts K4,4.

How many Hamiltonian paths are there in K4,4 starting from a particular node s in one partition and ending in a particular node t in the other partition? 2. Suppose that we remove the edge (s, t) from K4,4. How many Hamiltonian paths are there from s to t in the resulting graph? 3. Suppose that we remove the edge (s, v) from K4,4 where v = t. How many Hamiltonian paths are there from s to t in the resulting graph?

No Code Needed Need Only Answers with Detailed Explanation, please do NOT submit any code for above question. Only submit answers to the question. You may provide mathematical proofs/arguments for your answers