Suppose x(n) is obtained by sampling a continuous-time waveform x(t) with a sampling frequency of 128 Hz. This discrete time waveform x(n) can be represented using the Fourier series expansion, where N = 128.

 

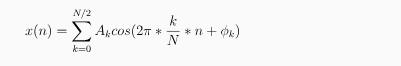
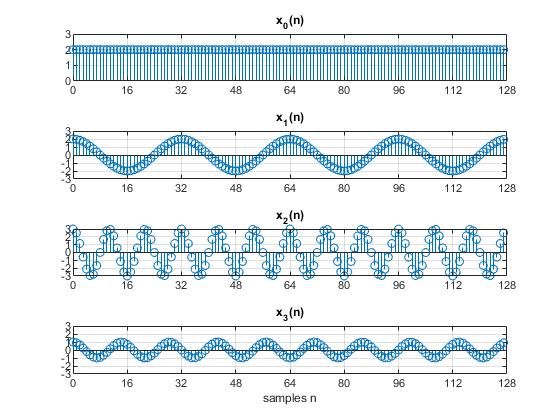
The frequency components of x(n) are the sum of all the x_s(n) as shown below, where s∈{0, 1, 2, 3}.

a) What is the Fourier Series expansion for x(n)? Assume: 

 

or all k.

b) Plot the amplitude spectrum of A_k versus frequency k for x(n). Clearly label all the values. (Please upload a jpg/png image)

c) Suppose we want you to design a filter system to block all the frequencies above 8 Hz. Draw and describe the important aspects of your filter. (Please upload a jpg/png image)

d) Suppose that the filtered signal y(t) is sampled with the same sampling frequency of 128 Hz, resulting in the discrete-time waveform y(n). What is the Fourier Series Expansion for the output y(n)?

Note: hand drawing is acceptable in parts B and C

=(n) = Arcos(2 k=0 N *ntek)