Suppose you are given a bipartite graph (L, R, E), where L denotes the vertices on the left, R denotes the vertices on the right and E denote the set of edges. Furthermore it is given that degree of every vertex is exactly d (you may assume that d > 0). We will construct a flow network G using this bipartite graph in the following manner: G has |L| + |R| + 2 vertices. There is a vertex corresponding to every vertex in L and R. There is also a source vertex s and a sink vertex t. There are directed edges with weight 1 from s to all vertices in L and directed edges of weight 1 from all vertices in R to t. For each edge (u, v) ? E, there is a directed edge from u to v with weight 1 in G. (The figure below shows an example of a bipartite graph and the construction of the network.)

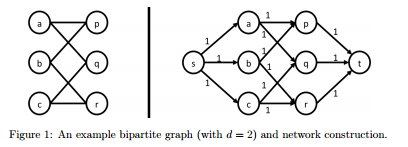
Argue that for any such bipartite graph where the degree of every vertex is equal to d, |L| is equal to |R|.

Figure 1: An example bipartite graph (with d-2) and network construction