) Suppose you have a two-species dynamical model, where one species is a predator and the other is a prey. The population sizes of prey and predator at time t are denoted N(t) and P(t), respectively. You calculate that the coexistence equilibrium, denoted {N*, P*} exists, and the eigenvalues of the Jacobian matrix, evaluated at the coexistence equilibrium, are: 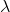= 0.5 0.1i, where i = 1. If the state of the system (i.e. the population sizes, N(t), P(t)) were pushed a tiny distance away from the coexistence equilibrium, what would happen next?

a. The state of the system {N(t), P(t)} would move straight back to the equilibrium {N*, P*}.

b. The state of the system {N(t), P(t)} would move straight away from the equilibrium {N*, P*}.

c. The state of the system {N(t), P(t)} would cycle inward towards the equilibrium {N*, P*}.

d. The state of the system {N(t), P(t)} would cycle outward away from the equilibrium {N*, P*}.

e. We dont have enough information to know what will happen.

Suppose you have a two-species dynamical model, where one species is a predator and the other is a prey. The population sizes of prey and predator at time t are denoted N(t) and Plt), respectively. You calculate that the coexistence equilibrium, denoted {N*, P*} exists, and the eigenvalues of the Jacobian matrix, evaluated at the coexistence equilibrium, are: 1 = -0.5 + 0.1i, where i = (-1. If the state of the system (i.e. the population sizes, N(t), P(t)) were pushed a tiny distance away from the coexistence equilibrium, what would happen next? a. The state of the system {N(t), P(t)} would move straight back to the equilibrium {N*, P*} b. The state of the system {N(t), P(t)} would move straight away from the equilibrium {N*, P*}. C. The state of the system {N(t), P(t)} would cycle inward towards the equilibrium {N*, p*}. d. The state of the system {N(t), P(t)} would cycle outward away from the equilibrium {N*, P*}. e. We don't have enough information to know what will happen. Suppose you have a two-species dynamical model, where one species is a predator and the other is a prey. The population sizes of prey and predator at time t are denoted N(t) and Plt), respectively. You calculate that the coexistence equilibrium, denoted {N*, P*} exists, and the eigenvalues of the Jacobian matrix, evaluated at the coexistence equilibrium, are: 1 = -0.5 + 0.1i, where i = (-1. If the state of the system (i.e. the population sizes, N(t), P(t)) were pushed a tiny distance away from the coexistence equilibrium, what would happen next? a. The state of the system {N(t), P(t)} would move straight back to the equilibrium {N*, P*} b. The state of the system {N(t), P(t)} would move straight away from the equilibrium {N*, P*}. C. The state of the system {N(t), P(t)} would cycle inward towards the equilibrium {N*, p*}. d. The state of the system {N(t), P(t)} would cycle outward away from the equilibrium {N*, P*}. e. We don't have enough information to know what will happen