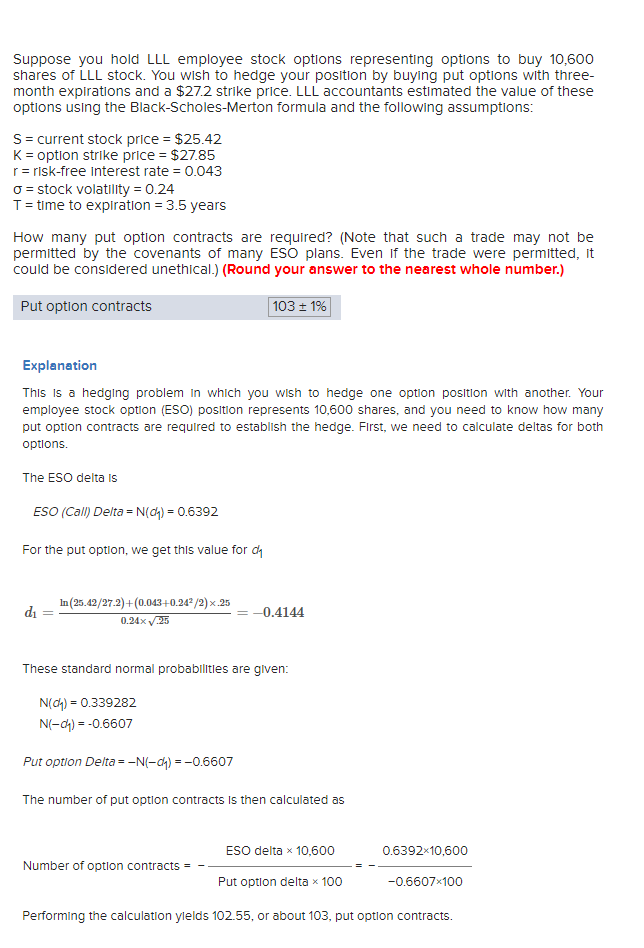
Question
Suppose you hold LLL employee stock options representing options to buy 10,700 shares of LLL stock. You wish to hedge your position by buying put
| Suppose you hold LLL employee stock options representing options to buy 10,700 shares of LLL stock. You wish to hedge your position by buying put options with three-month expirations and a $29.98 strike price. LLL accountants estimated the value of these options using the Black-Scholes-Merton formula and the following assumptions: |
| S = current stock price = $28.2 |
| K = option strike price = $30.63 |
| r = risk-free interest rate = 0.032 |
| = stock volatility = 0.24 |
| T = time to expiration = 3.5 years |
| How many put option contracts are required? (Note that such a trade may not be permitted by the covenants of many ESO plans. Even if the trade were permitted, it could be considered unethical.) (Round your answer to the nearest whole number.) |
| Put option contracts |
Here is an explanation of a similar problem:
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


