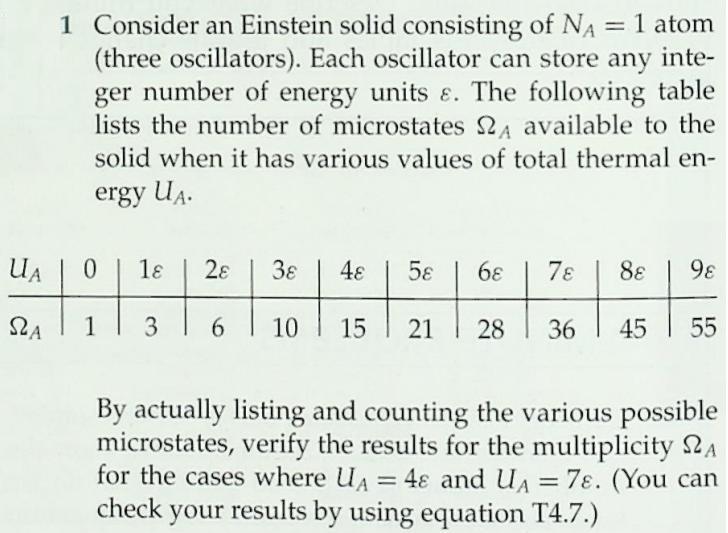
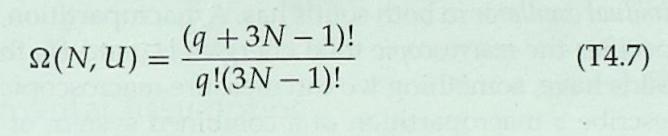
1 Consider an Einstein solid consisting of NA = 1 atom (three oscillators). Each oscillator can store any inte- ger number of energy units . The following table lists the number of microstates 2A available to the %3D solid when it has various values of total thermal en- ergy UA. UA 0. 1 38 48 5 6 78 8 98 1 SLA 6. 10 15 21 28 36 45 55 By actually listing and counting the various possible microstates, verify the results for the multiplicity 2A for the cases where UA = 4 and UA = check your results by using equation T4.7.) 78. (You can %3D 3. T4S.2 Consider an Einstein solid consisting of NB =2 atoms. The following table lists the number of microstates 2B available to the solid when it has various values of total internal energy UB. UB | 0 1 28 48 5 6 78 88 9 S2B | 1 21 56 126 | 252 | 462 792 1287 2002 (a) By actually listing the various possible mi- crostates, verify the result for UB = 2. (b) Using equation T4.7, verify the value of 2B for UB = 6 and 9. %3D T4S.3 Imagine putting the two solids discussed in problems T4S.1 and T4S.2 into thermal contact. Imagine that the resulting combined system is isolated from every- thing else, and that the combined system contains 6 units of energy (that is, UA + UB = 6). (a) Construct a table showing UA, UB, SA, SB, and LAB for all possible macropartitions of the system (i.e., a table analogous to table T4.1), and com- pute the probabilities for each of the seven possi- ble macropartitions according to the fundamental assumption. (b) Identify the most probable macropartition(s) of this system. Is the energy evenly divided between the solids in the most probable macropartition(s)? %3D Table T4.1 Possible macropartitions for NA = NB =1, U = 6 %3D Macropartition UA UB SZA SB SLAB 0:6 0. 1 28 28 1:5 1 3 21 63 2:4 2 15 90 3:3 3 10 10 100 4:2 4 15 6. 90 5:1 21 3 63 6:0 6. 28 1 28 Grand total number of microstates = 462 6 54 m21 (9+3N 1)! 9!(3N 1)! 2(N, U) = (T4.7) %3D