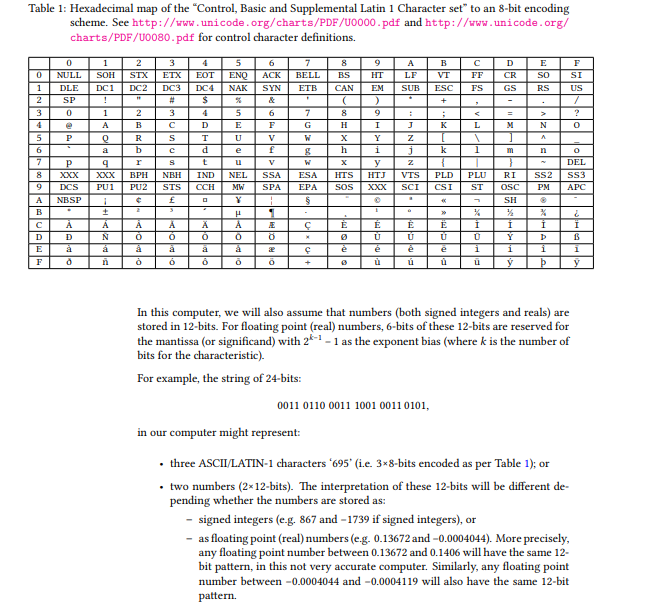
?

Table 1: Hexadecimal map of the "Control, Basic and Supplemental Latin 1 Character set" to an 8-bit encoding scheme. See http://www.unicode.org/charts/PDF/U0000.pdf and http://www.unicode.org/ charts/PDF/U0080.pdf for control character definitions. LF SI DLE DC1 DC2 DC3 | DC4 NAK SYN ETB CAN EM SUB ESC FS GS RS SP 0 DEL SS2 SS3 PM APC DCS PU1 PU2STSC CCH MW SPA EPA SOS XxX SCI CSI A NBSP 0 0 In this computer, we will also assume that numbers (both signed integers and reals) are stored in 12-bits. For floating point (real) numbers, 6-bits of these 12-bits are reserved for the mantissa (or significand) with 21-1 as the exponent bias (where k is the number of bits for the characteristic). For example, the string of 24-bits: 0011 0110 0011 1001 0011 0101, in our computer might represent three ASCIL LATIN-1 characters '695, (i.e. 3x8-bits encoded as per Table 1); or two numbers (2x12-bits). The interpretation of these 12-bits will be different de- pending whether the numbers are stored as: signed integers (e.g. 867 and -1739 if signed integers), or as floating point (real) numbers (e.g. 0.13672 and -0.0004044). More precisely any floating point number between 0.13672 and 0.1406 will have the same 12- bit pattern, in this not very accurate computer. Similarly, any floating point number between -0.0004044 and -0.0004119 will also have the same 12-bit pattern Table 1: Hexadecimal map of the "Control, Basic and Supplemental Latin 1 Character set" to an 8-bit encoding scheme. See http://www.unicode.org/charts/PDF/U0000.pdf and http://www.unicode.org/ charts/PDF/U0080.pdf for control character definitions. LF SI DLE DC1 DC2 DC3 | DC4 NAK SYN ETB CAN EM SUB ESC FS GS RS SP 0 DEL SS2 SS3 PM APC DCS PU1 PU2STSC CCH MW SPA EPA SOS XxX SCI CSI A NBSP 0 0 In this computer, we will also assume that numbers (both signed integers and reals) are stored in 12-bits. For floating point (real) numbers, 6-bits of these 12-bits are reserved for the mantissa (or significand) with 21-1 as the exponent bias (where k is the number of bits for the characteristic). For example, the string of 24-bits: 0011 0110 0011 1001 0011 0101, in our computer might represent three ASCIL LATIN-1 characters '695, (i.e. 3x8-bits encoded as per Table 1); or two numbers (2x12-bits). The interpretation of these 12-bits will be different de- pending whether the numbers are stored as: signed integers (e.g. 867 and -1739 if signed integers), or as floating point (real) numbers (e.g. 0.13672 and -0.0004044). More precisely any floating point number between 0.13672 and 0.1406 will have the same 12- bit pattern, in this not very accurate computer. Similarly, any floating point number between -0.0004044 and -0.0004119 will also have the same 12-bit pattern