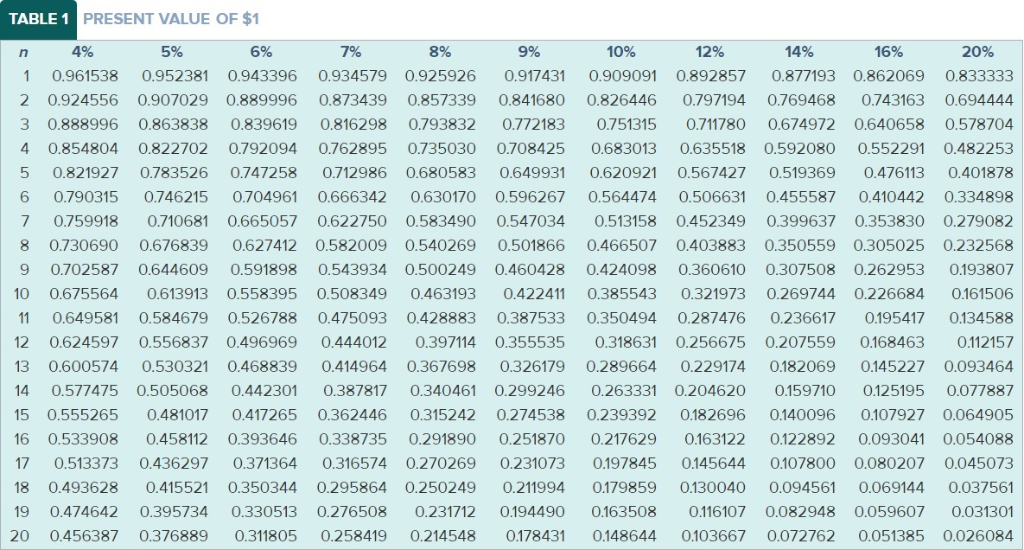
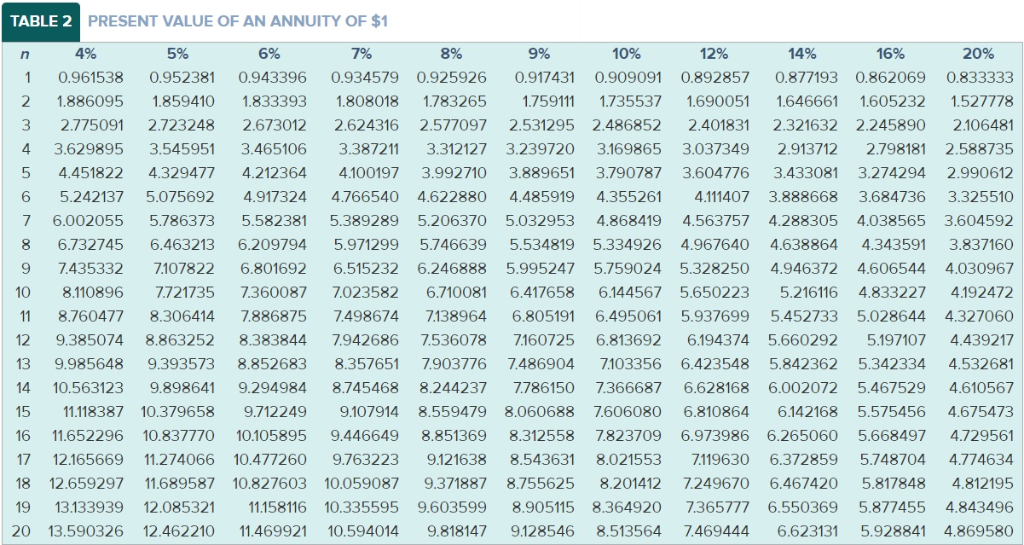
TABLE 1 PRESENT VALUE OF $1 4% 5% 6% 7% 8% 9% 10% 12% 14% 16% 20% 0.961538 0.943396 0.917431 0.892857 1 0.952381 0.934579 0.925926 0.909091 0.877193 0.862069 0.833333 0.924556 0.907029 0.873439 0.857339 0.841680 0.826446 0.769468 0.889996 0.797194 0.743163 0.694444 3 0.888996 0.863838 0.839619 0.816298 0.793832 0.772183 0.751315 0.711780 O.674972 0.640658 0.578704 0.854804 0.822702 0.792094 0.762895 0.708425 0,635518 0.592080 0.482253 4 0.735030 0.683013 0.552291 0.821927 O.783526 0.680583 0.649931 0.401878 0.747258 O.712986 0.620921 0.567427 0.519369 0.476113 0,704961 0.790315 0.596267 0.506631 0.455587 6 O.746215 0.666342 0.630170 0.564474 0.410442 0.334898 0.759918 0.710681 0.583490 0.547034 0.279082 0.665057 0.622750 0.513158 0.452349 0.399637 0.353830 0.730690 0.676839 0.627412 0.350559 0.582009 0.540269 0.501866 0.466507 0.403883 0.305025 0.232568 0.591898 0.307508 O.702587 0.543934 0.500249 0.460428 0.424098 0.262953 0.644609 0.360610 0.193807 0.558395 0.508349 0.463193 0.422411 0.321973 0.269744 1C 0.675564 0.613913 0.385543 0.226684 0.161506 0.526788 0.428883 0.387533 0.236617 0.195417 11 0.649581 0.584679 0.475093 0.350494 0.287476 0.134588 0.496969 0.397114 0.256675 0.168463 12 0.624597 0.556837 0.444012 0.355535 0.318631 0.207559 0.112157 0.600574 0.468839 0.367698 13 0.530321 0.414964 0.326179 0.289664 0.229174 0.182069 0.145227 0.093464 0.442301 0.577475 0.505068 0.299246 0.125195 14 0.387817 0.340461 0.263331 0.204620 0.159710 O.077887 15 0.481017 0.315242 0.274538 0.182696 0.140096 0.555265 0.417265 0.362446 0.239392 0.107927 0.064905 0.393646 0.251870 0.163122 0.122892 0.054088 16 0.533908 0.458112 0.338735 0.291890 0.217629 0.093041 17 373 97 69 73 800 0.08 73 0.415521 0.350344 0.211994 0.179859 0.130040 O.037561 18 0.493628 0.295864 0.2 50249 0.094561 0.069144 0.474642 0.276508 0.194490 0.163508 0.059607 19 0.395734 0.330513 0.231712 0.116107 0.082948 0.031301 20 0.456387 0.311805 0.214548 0.178431 0.103667 O.072762 0.376889 0.258419 0.148644 0.051385 0.026084 TABLE 2 PRESENT VALUE OF AN ANNUITY OF $1 4% 5% 6% 7% 8% 9% 10% 12% 14% 16% 20% n 0.909091 0.961538 0.952381 0.943396 0.934579 0.925926 0.917431 0.892857 0,877193 0.862069 0.833333 1.859410 1.783265 1.646661 1.886095 1.833393 1.808018 1.759111 1.735537 1.690051 1.605232 1.527778 2 2.723248 2.624316 2.486852 3 2.775091 2.673012 2.577097 2.531295 2.401831 2.321632 2.245890 2.106481 3.545951 3.465106 4 3.629895 3.387211 3.312127 3.239720 3.169865 3.037349 2.913712 2.798181 2.588735 4.212364 4.100197 3.992710 3.889651 3.604776 4.451822 4.329477 3.790787 3.433081 3.274294 2.990612 5.075692 4.622880 4.485919 3.888668 3.325510 6 5.242137 4.917324 4.766540 4.355261 4.111407 3.684736 4,868419 3.604592 5.786373 5.032953 4.563757 7 6.002055 5.582381 5.389289 5.206370 4.288305 4.038565 6,463213 4.343591 6.209794 5.534819 CO 6.732745 5.971299 5.746639 5.334926 4.967640 4.638864 3.837160 7.107822 6.515232 7.435332 6.801692 6.246888 5.995247 5.759024 5.328250 4,606544 4.946372 4.030967 4.833227 7.721735 7.360087 7.023582 5.650223 10 8.110896 6.710081 6.417658 6.144567 5.216116 4.192472 8.760477 7.138964 5.028644 11 8.306414 7.886875 7.498674 6.805191 6.495061 5.937699 5.452733 4.327060 9.385074 7:160725 5.660292 5.197107 12 8.863252 8.383844 7.942686 7.536078 6.813692 6.194374 4.439217 7.903776 9,393573 8.357651 5.842362 4.532681 13 9.985648 .852683 7.486904 7.103356 6.423548 5.342334 9,898641 9.294984 8.244237 7.366687 6.628168 4.610567 14 10.563123 8.745468 7.786150 6.002072 5.467529 11.118387 10.379658 9.107914 4.675473 15 9.712249 8.559479 8.060688 7.606080 6.810864 6.142168 5.575456 8.851369 16 11.652296 10.837770 10.105895 9.446649 8.312558 7.823709 6.973986 6.265060 5.668497 4.729561 9.763223 9.121638 4.774634 12.165669 8.543631 8.021553 7.119630 6.372859 5.748704 17 11.274066 10.477260 12.659297 10.059087 7.249670 11.689587 9.371887 .755625 8.201412 6.467420 5.817848 4.812195 18 10.827603 9.603599 13.133939 12.085321 6.550369 19 11.158116 10.335595 8.905115 8.364920 7.365777 5.877455 4.843496 11.469921 20 13.590326 12.462210 10.594014 9.818147 9.128546 8.513564 7.469444 6.623131 5.928841 4.869580 In recent years, there has been a lot of media coverage about the funding status of pension plans for state employees. In many states, the amount of money invested in employee pension plans is far less than the amount estimated to pay employees the retirement benefits they have been promised. Basically, pension plans work by investing enough money while employees are working so that the money invested, plus the investment income it earns over the years, will be sufficient to pay the workers their retirement incomes once they have retired. There are many complicated assumptions, estimates, and calculations needed to determine how much money a state should invest in its pension fund each year. One of the most important assumptions is the rate of return the plan's investments will earn in the future. As you have seen in this chapter, the higher the rate of return used to calculate the present value of future cash flows, the lower the present value will be. To determine a pension plan's funded status, actuaries (1) estimate the future cash payments expected to be made to employees, (2) calculate the present value of those cash flows using an assumed rate of return (this present value is the gross liability of the fund), and (3) subtract the amount of money that has been invested from the gross liability calculated in step 2 (this amount is the funded status of the pension plan). Essentially, this is the same as calculating the net present value of an investment. If the plan has less money in its investments than the present value of its estimated future cash flows, it has a net liability and is considered to be underfunded by that amount. Many states' pension plans have assumed they will earn 6 percent or more on their investments, even though many experts think a more appropriate assumption would be 4.5 percent. As an example, the state of Virginia used an assumed rate of return of 5.5 percent in 2009 but reduced the rate to 6.0 percent in 2011. In 2014, Virginia paid out approximately $4.0 billion in benefits to retirees. (PV of $1 and PVA of $1) (Use appropriate factor(s) from the tables provided.) Required a. Assume Virginia's annual payments will continue to be $4.0 billion, and that retirees will receive benefits for 20 years on average. Using an assumed rate of return of 6 percent, calculate the liability of the state's pension plan. The liability is the present value of the future cash payments. (Be aware that the real-world calculation for a state's pension plan liability involves many more assumptions than just these two.) b. Assume the annual payments will continue to be $4.0 billion, and that retirees will receive benefits for 20 years on average. Using an assumed rate of return of 4 percent, calculate the liability of the state's pension plan. Required a. Assume Virginia's annual payments will continue to be $4.0 billion, and that retirees will receive benefits for 20 years on average. Using an assumed rate of return of 6 percent, calculate the liability of the state's pension plan. The liability is the present value of the future cash payments. (Be aware that the real-world calculation for a state's pension plan liability involves many more assumptions than just these two.) b. Assume the annual payments will continue to be $4.0 billion, and that retirees will receive benefits for 20 years on average. Using an assumed rate of return of 4 percent, calculate the liability of the state's pension plan. (For all requirements, enter your answers in dollars not in billions.) Gross Pension Liability a. b. Espada Real Estate Investment Company (EREIC) purchases new apartment complexes, establishes a stable group of residents, and then sells the complexes to apartment management companies. The average holding time is three years. EREIC is currently investigating two alternatives. (PV of $1 and PVA of $1) (Use appropriate factor(s) from the tables provided.) 1. EREIC can purchase Harding Properties for $4,590,000. The complex is expected to produce net cash inflows of $367,200, $512,600, and $882,500 for the first, second, and third years of operation, respectively. The market value of the complex at the end of the third year is expected to be $5,279,700. 2. EREIC can purchase Summit Apartments for $3,519,800. The complex is expected to produce net cash inflows of $295,900 $444,000, and $612,500 for the first, second, and third years of operation, respectively. The market value of the complex at the end of the third year is expected to be $4,130,000. EREIC has a desired rate of return of 10 percent. Required a-1. Calculate the net present value and the present value index for Harding Properties. a-2. Calculate the net present value and the present value index for Summit Apartments. b. Which investment opportunity should be taken? (For all requirements, round "Present Value" to the nearest whole dollar amount. Round "Present value index" to 2 decimal places.) Harding Properties Apartments Summit a-1. Net present value a-2. Present value index Which investment opportunity should be taken? b