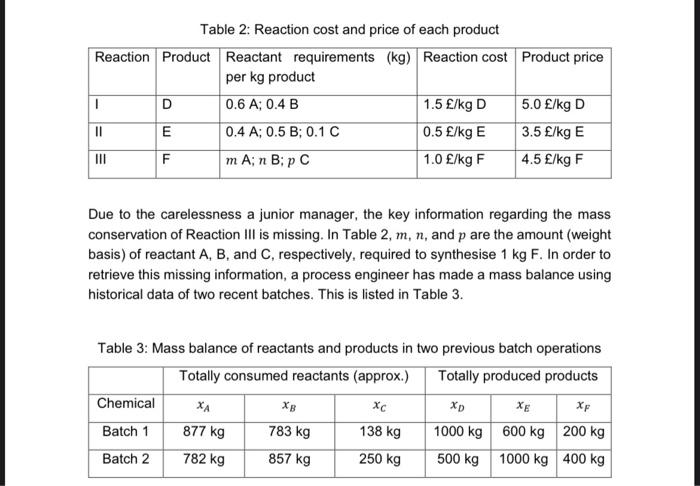
Table 2: Reaction cost and price of each product Reaction Product Reactant requirements (kg) Reaction cost Product price per kg product ! D 0.6 A; 0.4 B 1.5 /kg D 5.0 /kg D 11 E 0.4 A; 0.5 B: 0.1 C 0.5 /kg E 3.5 /kg E F mA; n B:p C 1.0 /kg F 4.5 /kg F Due to the carelessness a junior manager, the key information regarding the mass conservation of Reaction III is missing. In Table 2, m, n, and p are the amount (weight basis) of reactant A, B, and C, respectively, required to synthesise 1 kg F. In order to retrieve this missing information, a process engineer has made a mass balance using historical data of two recent batches. This is listed in Table 3. Table 3: Mass balance of reactants and products in two previous batch operations Totally consumed reactants (approx.) Totally produced products Chemical XA XE Xp Batch 1 877 kg 783 kg 138 kg 1000 kg 600 kg 200 kg Batch 2 782 kg 857 kg 250 kg 500 kg 1000 kg 400 kg . 2. Least-squares model construction (5 marks): 2.1. Use only Table 2 and Table 3 to construct a full least-squares model with an objective to calculate m, n, and p. You can only build the model using: XA1 (kg day of A consumed in batch 1), X8,1 (kg day of B consumed in batch 1), Xc1 (kg day of C consumed in batch 1), XA2 (kg day of A consumed in batch 2), XB:2 (kg day of B consumed in batch 2), Xcz (kg day of C consumed in batch 2), m, n, and p. No other symbols are allowed to use. The full model should consist of both an objective function and all possible constraints - remember that all constraints, as well as the objective function, should be independent from each other. Note: Do not use the 'normalised least-squares objective function. 2.2. Restructure the full optimisation model in 2.1 into a reduced optimisation model by substituting the equality constraints where appropriate. Make sure the reduced model only consists of inequality constraints. The reduced model should consist of both an objective function and all possible inequality constraints. Note: Do not use the 'normalised' least-squares objective function. Table 2: Reaction cost and price of each product Reaction Product Reactant requirements (kg) Reaction cost Product price per kg product ! D 0.6 A; 0.4 B 1.5 /kg D 5.0 /kg D 11 E 0.4 A; 0.5 B: 0.1 C 0.5 /kg E 3.5 /kg E F mA; n B:p C 1.0 /kg F 4.5 /kg F Due to the carelessness a junior manager, the key information regarding the mass conservation of Reaction III is missing. In Table 2, m, n, and p are the amount (weight basis) of reactant A, B, and C, respectively, required to synthesise 1 kg F. In order to retrieve this missing information, a process engineer has made a mass balance using historical data of two recent batches. This is listed in Table 3. Table 3: Mass balance of reactants and products in two previous batch operations Totally consumed reactants (approx.) Totally produced products Chemical XA XE Xp Batch 1 877 kg 783 kg 138 kg 1000 kg 600 kg 200 kg Batch 2 782 kg 857 kg 250 kg 500 kg 1000 kg 400 kg . 2. Least-squares model construction (5 marks): 2.1. Use only Table 2 and Table 3 to construct a full least-squares model with an objective to calculate m, n, and p. You can only build the model using: XA1 (kg day of A consumed in batch 1), X8,1 (kg day of B consumed in batch 1), Xc1 (kg day of C consumed in batch 1), XA2 (kg day of A consumed in batch 2), XB:2 (kg day of B consumed in batch 2), Xcz (kg day of C consumed in batch 2), m, n, and p. No other symbols are allowed to use. The full model should consist of both an objective function and all possible constraints - remember that all constraints, as well as the objective function, should be independent from each other. Note: Do not use the 'normalised least-squares objective function. 2.2. Restructure the full optimisation model in 2.1 into a reduced optimisation model by substituting the equality constraints where appropriate. Make sure the reduced model only consists of inequality constraints. The reduced model should consist of both an objective function and all possible inequality constraints. Note: Do not use the 'normalised' least-squares objective function