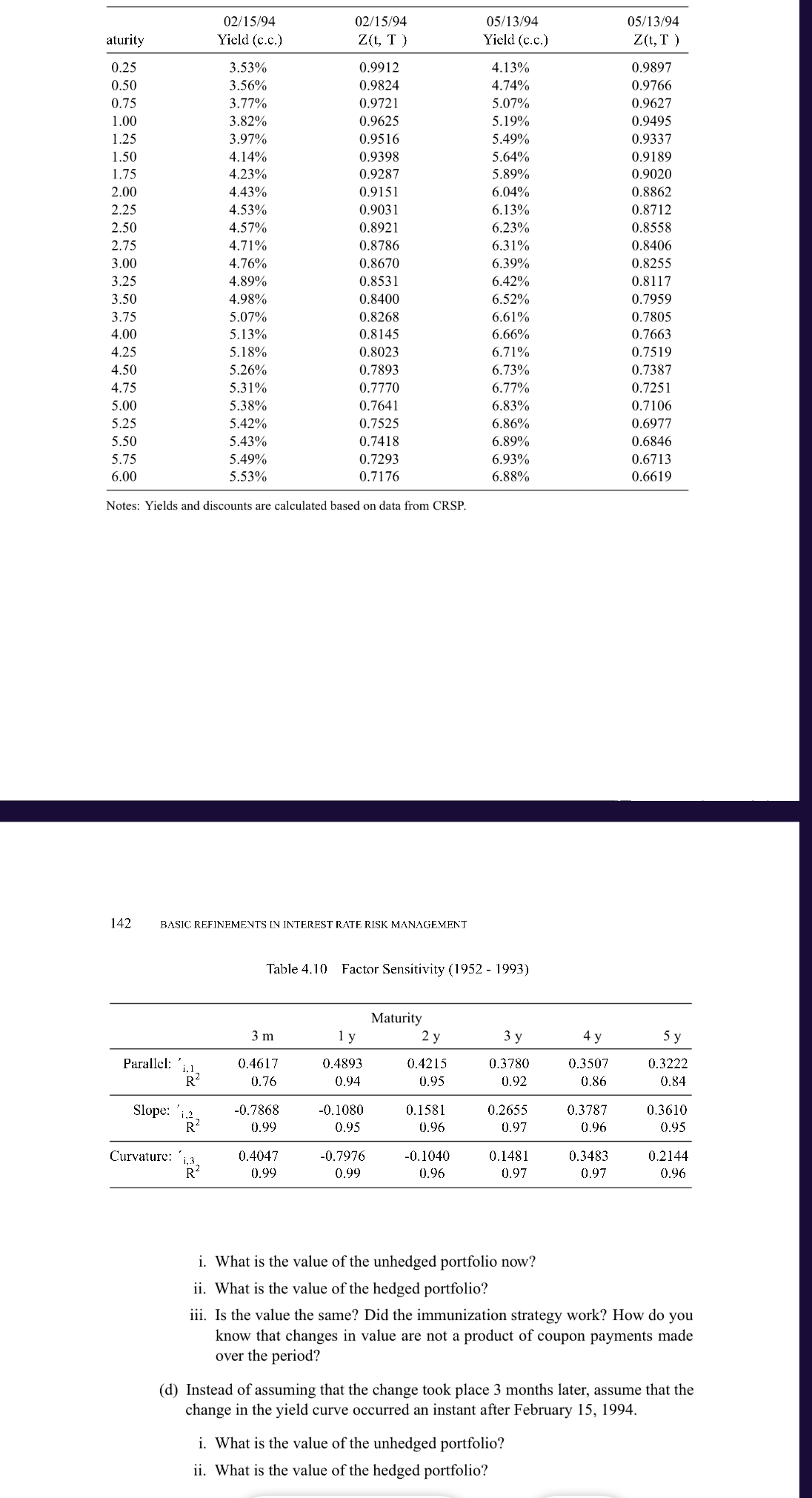
Table 4.8 Level, Slope and Curvature 3 month 6 month 1 year 2 year 7 year 10 year 1.0111 1.0180 ' (Level) 1.0344 1.0299 -0.3507 -0.1424 1.0180 0.2432 0.5205 0.7432 1.0180 0.9509 0.9196 (Slope) -0.2568 -0.3252 -0.4317 (Curvature) -0.3284 -0.1404 0.0847 0.3228 0.3240 0.1716 -0.1058 -0.3284 R 99.65% 99.69% 98.88% 99.61% 99.77% 99.90% 99.73% 99.90% 3 year 5 year 8. In this exercise you need to describe an immunization strategy for a portfolio, given the factors in Table 4.8. The term structures of interest rates at two dates are in Table 4.9. (a) You are standing at February 15, 1994 (see table) and you hold the following portfolio: Long $30 million of a 6-year inverse floater with coupon paid quarterly Long $30 million of a 4-year floating rate bond with a 45 basis point spread paid semiannually Short $20 million of a 3-year coupon bond paying 4% semiannually i. What is the total value of the portfolio? ii. Compute the dollar duration of the portfolio. (b) You are worried about interest rate volatility. You decided to hedge your portfolio with the following bonds: A 3-month zero coupon bond A 6-year zero coupon bond i. How much should you go short/long on these bonds in order to make the portfolio immune to interest rate changes? ii. What is the total value of the portfolio now? (c) Assume that it is now May 13, 1994 and that the yield curve has changed accordingly. aturity 0.25 0.50 0.75 1.00 1.25 1.50 1.75 2.00 2.25 2.50 2.75 3.00 3.25 3.50 3.75 4.00 4.25 4.50 4.75 5.00 5.25 Parallel: ' i.l Curvature: R Slope: 2 R 02/15/94 Yield (c.c.) 5.50 5.75 6.00 Notes: Yields and discounts are calculated based on data from CRSP. 3.53% 3.56% i,3. 3.77% 3.82% 3.97% 4.14% 4.23% 4.43% 4.53% 4.57% 4.71% 4.76% 4.89% 4.98% 5.07% 5.13% 5.18% 5.26% 5.31% 5.38% 142 BASIC REFINEMENTS IN INTEREST RATE RISK MANAGEMENT 5.42% 5.43% 5.49% 5.53% 02/15/94 Z(t, T) 3 m 0.4617 0.76 0.9912 0.9824 0.9721 0.9625 0.9516 0.9398 0.9287 0.9151 0.9031 0.8921 0.8786 0.8670 0.8531 0.8400 0.8268 0.8145 0.8023 0.7893 0.7770 0.7641 0.7525 0.7418 0.7293 0.7176 -0.7868 0.99 0.4047 0.99 Table 4.10 Factor Sensitivity (1952 - 1993) 1 y 0.4893 0.94 -0.1080 0.95 -0.7976 0.99 Maturity 2 y 0.4215 0.95 0.1581 0.96 05/13/94 Yield (c.c.) -0.1040 0.96 4.13% 4.74% 5.07% 5.19% 5.49% 5.64% 5.89% 6.04% 6.13% 6.23% 6.31% 6.39% 6.42% 6.52% 6.61% 6.66% 6.71% 6.73% 6.77% 6.83% 6.86% 6.89% 6.93% 6.88% 3 y 0.3780 0.92 0.2655 0.97 0.1481 0.97 4 y 0.3507 0.86 0.3787 0.96 i. What is the value of the unhedged portfolio? ii. What is the value of the hedged portfolio? 0.3483 0.97 05/13/94 Z(t, T) 0.9897 0.9766 0.9627 0.9495 0.9337 0.9189 0.9020 0.8862 0.8712 0.8558 0.8406 0.8255 0.8117 0.7959 0.7805 0.7663 0.7519 0.7387 0.7251 0.7106 0.6977 0.6846 0.6713 0.6619 5 y 0.3222 0.84 0.3610 0.95 0.2144 0.96 i. What is the value of the unhedged portfolio now? ii. What is the value of the hedged portfolio? iii. Is the value the same? Did the immunization strategy work? How do you know that changes in value are not a product of coupon payments made over the period? (d) Instead of assuming that the change took place 3 months later, assume that the change in the yield curve occurred an instant after February 15, 1994.