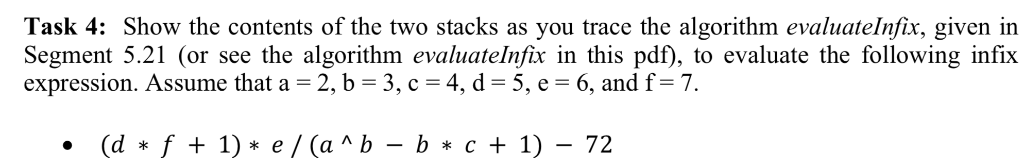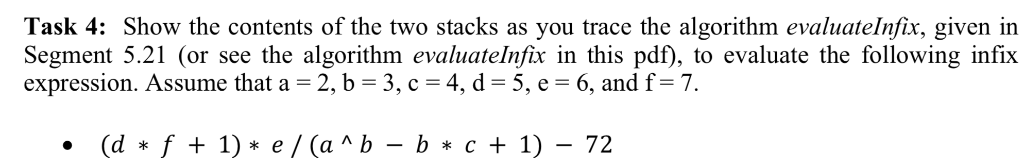
Task 4: Show the contents of the two stacks as you trace the algorithm evaluatelnfix, given in Segment 5.21 (or see the algorithm evaluatelnfix in this pdf), to evaluate the following infix expression. Assume that a -2, b-3, c 4, d- 5, e 6, and f-7. .(df + 1)* e / (a A b - b* c+ 1) - 72 2. The algorithm convertToPostfix Algorithm convertToPostfix(infix) Converts an infix expression to an equivalent postfix expression operatorStack a new empty stack postfix-anew empty string while Cinfix has characters left to parse) nextCharacter next nonblank character of infix switch (nextCharacter) case variable Append nextCharacter to postfix break case 'A operatorStack.push(nextCharacter) break case'casecase case' while (loperatorStack.isEmptyO and precedence of nextCharacterprecedence of operatorStack.peek O Append operatorStack.peek O to postfix operatorStack.popO operatorStack.push(nextCharacter) break case operatorStack.push(nextCharacter) break case / stack is not empty if infix expression is valid topoperator = operatorStack.popC) while (topOperator-" Append topOperator to postfix topOperator-operatorStack.popO break default: break while CloperatorStack.isEmptyO topOperator operatorStack.pop Append topOperator to postfix return postfix Task 4: Show the contents of the two stacks as you trace the algorithm evaluatelnfix, given in Segment 5.21 (or see the algorithm evaluatelnfix in this pdf), to evaluate the following infix expression. Assume that a -2, b-3, c 4, d- 5, e 6, and f-7. .(df + 1)* e / (a A b - b* c+ 1) - 72 2. The algorithm convertToPostfix Algorithm convertToPostfix(infix) Converts an infix expression to an equivalent postfix expression operatorStack a new empty stack postfix-anew empty string while Cinfix has characters left to parse) nextCharacter next nonblank character of infix switch (nextCharacter) case variable Append nextCharacter to postfix break case 'A operatorStack.push(nextCharacter) break case'casecase case' while (loperatorStack.isEmptyO and precedence of nextCharacterprecedence of operatorStack.peek O Append operatorStack.peek O to postfix operatorStack.popO operatorStack.push(nextCharacter) break case operatorStack.push(nextCharacter) break case / stack is not empty if infix expression is valid topoperator = operatorStack.popC) while (topOperator-" Append topOperator to postfix topOperator-operatorStack.popO break default: break while CloperatorStack.isEmptyO topOperator operatorStack.pop Append topOperator to postfix return postfix