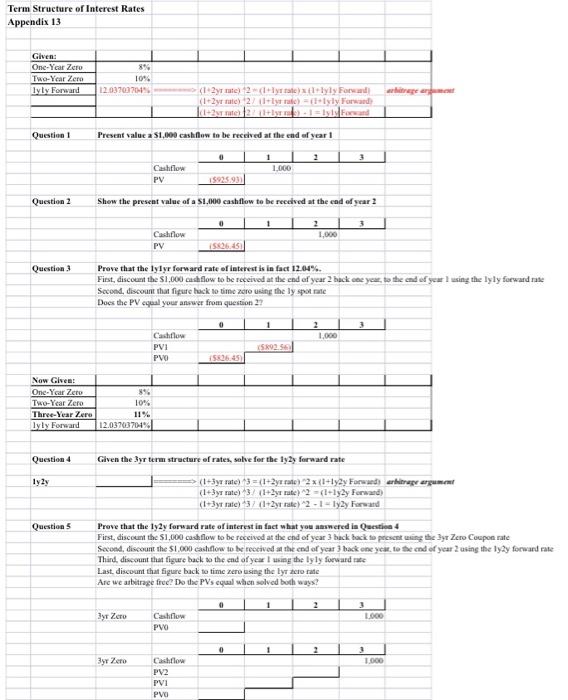
Term Structure of Interest Rates Appendix 13 Given: One-Year Zero Two-Year Zero Tyly Forward 8% 10% 12.037037049 are a (1-2yr mate) 2-lyreillyly Forward (1+2yrte 2 lytrade) sly Forward 11+By Feed Question 1 Present value 2 51,000 cash flow to be received at the end of year 1 0 2 3 Cashflow PV 1 1.000 15925931 Question 2 Show the prescat value of a $1.000 cash flow to be received at the end of year 2 0 1 3 2 1,000 Cashflow PV Question 3 Prove that the lylyr forward rate of interest is in fact 12.04%. Fiest, discount the $1,000 cashflow to be received at the end of year 2 back one year, to the end of yes 1 using the lyly forward rose Second, discount that figure luck to time 2010 using the lyspot rate Does the PV equal your answer from question 2? 0 1 3 1,000 Cashflow PVI PVO S9256 5245 Now Given: One-Year Zero 896 Two-Year Zero 10% Three-Year Zero 11% Lyly Forward 12.03703704% Question 4 Given the Syr term structure of rates, solve for the ly2y forward rate Iy2y Question 5 (1-3 yr rate) 3 = (1+2y rate) 2x{1+12y Forward arbitrage argument (1+3y rate) 37 (+2y rate)2 = +12y Forward (1+3yt rate) 37 (+2yt rate) 2 - 1 - Iy2y Forward Prove that the ly2y forward rate of interest in fact what you answered in Questina 4 First, discount the $1,000 cashflow to be received at the end of year 3 back back se presenting the Byt Zero Coupon rate Second, discount the $1.000 cashflow to be received at the end of year 3 back one year to be end of year 2 using the lygy forward rate Third, discount that figure back to the end of year I using the lyly forward rate Last discount that figure back to time zero using the lyrictorate Are we arbitrage frec? Do da PV's equal when solved both ways? 1 2 3yr Zero Cashflow PVO 1.000 0 3 3yx Zero 1.000 Cashflow PV2 PV1 PVO Given: One-Year Zero Two-Year Zero lyly Forward % 10% 12.037037047 arbitrage argomat > (1+2yrrate) 2-1 yr rate) (1 lyly Forward) (1-2yr rate) 2/(1+ly rate) - (l+lyty Forward |t+2yr rate) 27 (Itly rate) - 1 - Tyly Forward Question 1 Present value a $1,000 cash flow to be received at the end of year 1 0 2 3 1 1,000 Cashflow PV (592503 Question 2 Show the present value of a S1,000 cashflow to be received at the end of year 2 0 1 3 2 1.000 Cashflow PV (882645 Question 3 Prove that the lylyr forward rate of interest is in fact 12.04%. First, discount the $1,000 cashflow to be received at the end of year 2 hack one year, to the end of year I using the lyly forward rate Second, discount that figure back to time zero using the ly spot rate Does the PV equal your answer from question 2? 0 1 3 2 1.000 Cashflow PVI PVO (5892.56) (S82645) Now Given: One-Year Zero Two-Year Zero 10 Three-Year Zero 11% lyly Forward 12.03703704% Question 4 1y2y Questions Given the 3yr term structure of rates, solve for the ly2y forward rate (1 +3yr rate) *3 = (1-2yt rate) "2 x (H+ly2y Forward) arbitrage argument (1+3yr rate) 3 / (1+2yr rate) "2 = (1+ry2y Forward) (1+3yr rate) *3 / (1+2yt rate) 2 - 1 - 1y2y Forward Prove that the ly2y forward rate of interest in fact what you answered in Question 4 First, discount the $1.000 cashflow to be received at the end of year 3 back back to present using the 3yr Zero Cospon rate Second, discount the $1,000 cashflow to be received at the end of year 3 back one year, to the end of year 2 using the ly2y forward taste Third, discount that figure back to the end of year 1 using the lyly forward rate Last, discount that figure back to time zero using the lyr zero rate Are we arbitrage free? Do the PV's equal when solved both ways? 0 2 3 1.000 3yr Zero Cashflow PVO 0 1 2 Zero 3 1.000 Cashflow PV2 PV1 PVO