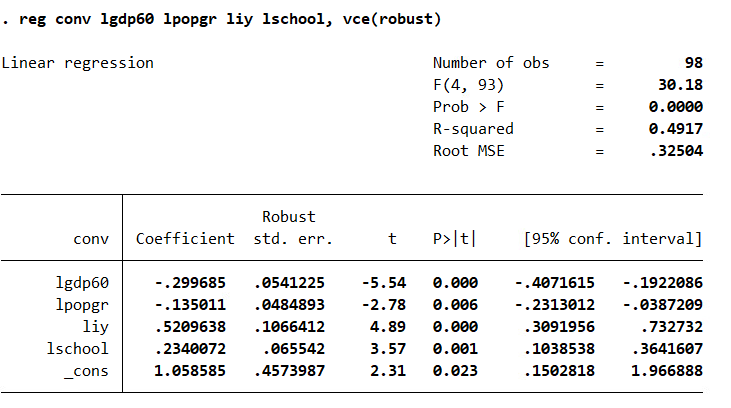
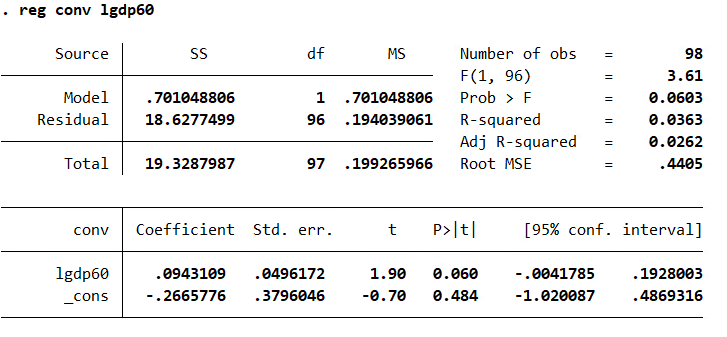
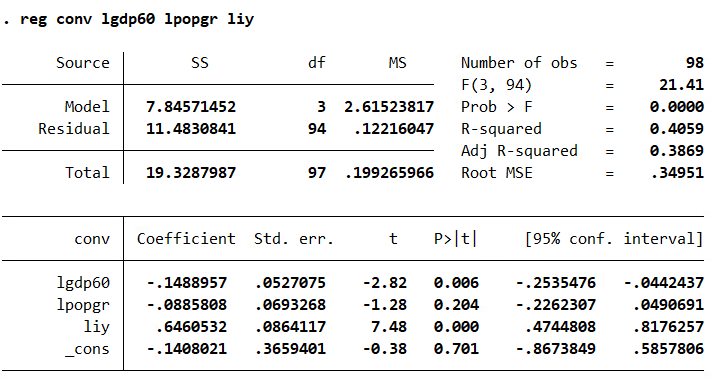
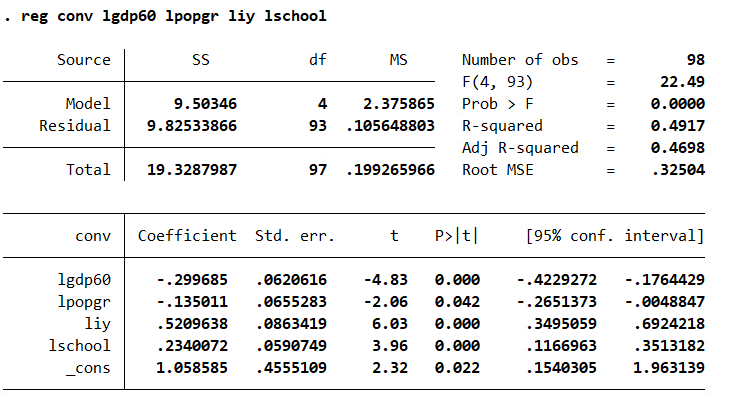
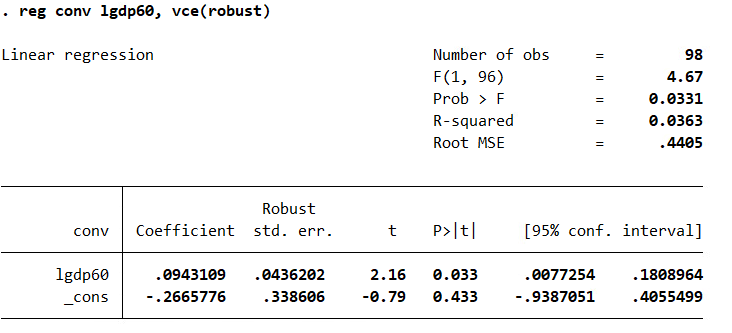
test whether there is a tendency for poor countries to converge with rich countries. Use the difference between LogGDP85 and LogGDP60 as the dependent variable. Use Table 5 and Table 6 to test whether poor countries tend to converge to rich countries (Use the difference between LogGDP85 and LogGDP60 as the dependent variable). In table 5, report results of unconditional convergence when no controls are used. In table 6 report results when controls are considered. Interpret your findings. Is the sign on the coefficient of Log (GDP60) consistent with expectations? Explain.

. reg conv lgdp60 1popgr liy 1school, vce (robust) Linear regression Number of obs = 98 F (4, 93) 30. 18 Prob > F = 0.0000 I R-squared = 0. 4917 Root MSE . 32504 Robust conv Coefficient std. err. t P>t [95% conf. interval] 1gdp50 - . 299685 . 0541225 -5.54 0.000 -. 4071615 - . 1922086 1popgr - . 135011 . 0484893 -2.78 0.006 - . 2313012 - . 0387209 liy . 5209638 . 1066412 4.89 0.000 . 3091956 . 732732 1school . 2340072 . 065542 3.57 0.001 . 1038538 . 3641607 cons 1.058585 . 4573987 2. 31 0. 023 . 1502818 1.966888. reg conv 1gdp50 Source SS df MS Number of obs 98 F(1, 96) 3.61 Model . 701048806 1 . 701048806 Prob > F = 0. 0603 Residual 18. 6277499 96 . 194039061 R-squared 0. 0363 Adj R-squared = 0. 0262 Total 19.3287987 97 . 199265966 Root MSE = . 4405 conv Coefficient Std. err. t P> t [95% conf. interval] 1gdp50 . 0943109 . 0496172 1.90 0. 060 - . 0041785 . 1928003 Cons - . 2665776 . 3796046 -0.70 0. 484 -1. 020087 . 4869316reg conv 1gdp50 1popgr liy Source SS df MS Number of obs = 98 F (3, 94) = 21. 41 Model 7.84571452 3 2.61523817 Prob > F = 0.0000 Residual 11. 4830841 94 . 12216047 R-squared = 0. 4059 Adj R-squared = 0. 3869 Total 19.3287987 97 . 199265966 Root MSE = . 34951 conv Coefficient Std. err. t [95% conf. interval] 1gdp50 - . 1488957 . 0527075 -2.82 0. 006 - . 2535476 - . 0442437 1popgr - . 0885808 . 0693268 -1.28 0. 204 - . 2262307 . 0490691 liy . 6460532 . 0864117 7.48 0.000 . 4744808 . 8176257 Cons - . 1408021 . 3659401 -0.38 0.701 - . 8673849 . 5857806. reg conv 1gdp50 1popgr liy 1school Source SS df MS Number of obs = 98 F (4, 93) = 22. 49 Model 9.50346 4 2.375865 Prob > F = 0.0000 Residual 9.82533866 93 . 105648803 R-squared = 0. 4917 Adj R-squared = 0. 4698 Total 19.3287987 97 . 199265966 Root MSE = . 32504 conv Coefficient Std. err. t P>/t| [95% conf. interval] 1gdp50 - . 299685 . 0620616 -4.83 0.000 - . 4229272 -.1764429 1popgr - . 135011 . 0655283 -2.06 0. 042 - . 2651373 - . 0048847 liy . 5209638 . 0863419 6.03 0.000 . 3495059 . 6924218 1school . 2340072 . 0590749 3.96 0.000 . 1166963 . 3513182 Cons 1. 058585 . 4555109 2.32 0. 022 . 1540305 1.963139. reg conv 1gdp50, vce (robust) Linear regression Number of obs = 98 F (1, 96) = 4.67 Prob > F = 0. 0331 R- squared = 0. 0363 Root MSE = . 4405 Robust conv Coefficient std. err. t P> t [95% conf. interval] 1gdp50 . 0943109 . 0436202 2.16 0. 033 . 0077254 . 1808964 cons - . 2665776 . 338606 -0.79 0.433 - .9387051 . 4055499reg conv 1gdp50 1popgr liy, vce(robust) inear regression Number of obs = 98 F (3, 94) = 24.00 Prob > F 0.0000 II R - squared 0. 4059 Root MSE = . 34951 Robust conv Coefficient std. err. t P> t [95% conf. interval] 1gdp50 - . 1488957 . 0491546 -3.03 0.003 - . 2464932 - . 0512981 1popgr - . 0885808 . 0505072 -1.75 0. 083 -. 188864 . 0117025 liy . 6460532 . 1028774 6. 28 0.000 . 4417877 . 8503188 Cons - . 1408021 . 3145477 -0.45 0. 655 765344 . 4837397