Thank you
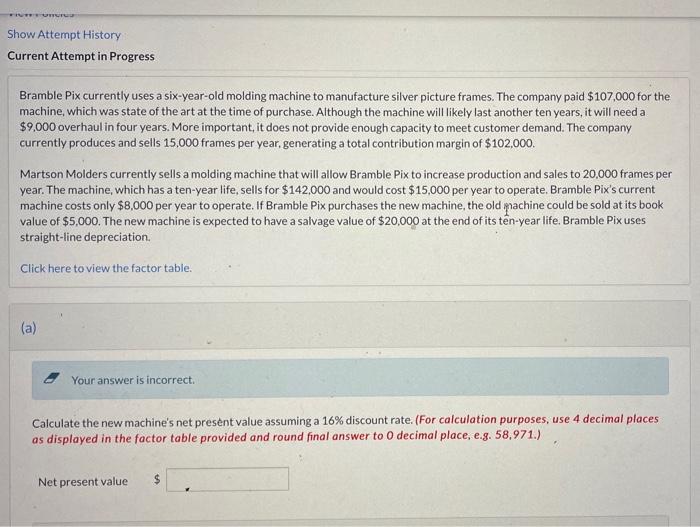
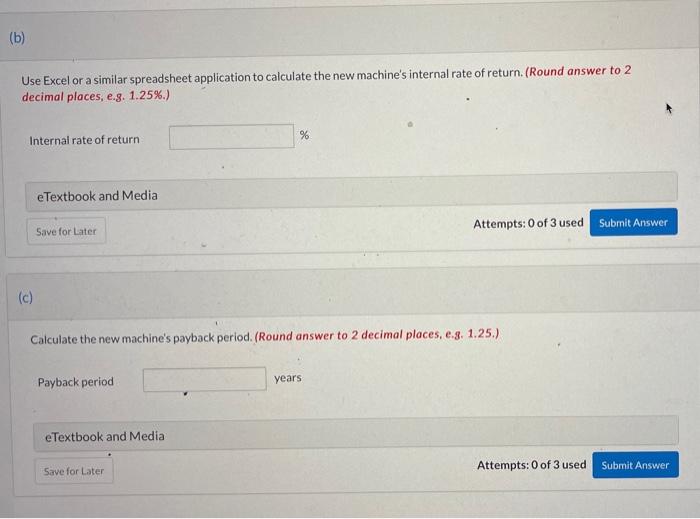
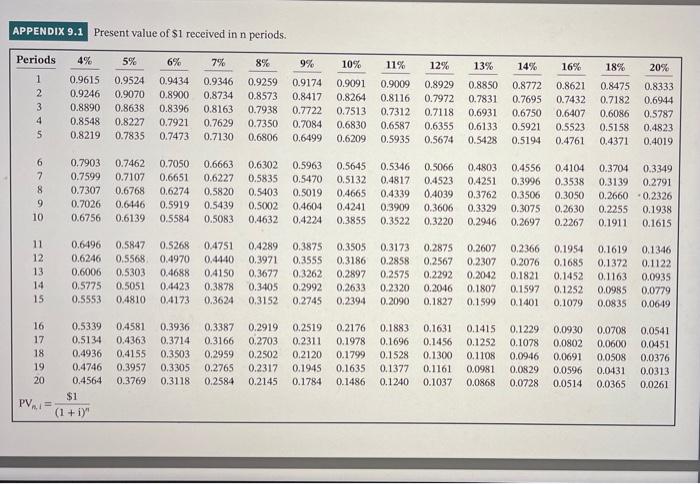
IN Show Attempt History Current Attempt in Progress Bramble Pix currently uses a six-year-old molding machine to manufacture silver picture frames. The company paid $107,000 for the machine, which was state of the art at the time of purchase. Although the machine will likely last another ten years, it will need a $9,000 overhaul in four years. More important, it does not provide enough capacity to meet customer demand. The company currently produces and sells 15,000 frames per year, generating a total contribution margin of $102,000. Martson Molders currently sells a molding machine that will allow Bramble Pix to increase production and sales to 20,000 frames per year. The machine, which has a ten-year life, sells for $142,000 and would cost $15,000 per year to operate. Bramble Pix's current machine costs only $8,000 per year to operate. If Bramble Pix purchases the new machine, the old machine could be sold at its book value of $5,000. The new machine is expected to have a salvage value of $20,000 at the end of its ten-year life. Bramble Pix uses straight-line depreciation Click here to view the factor table. (a) Your answer is incorrect. Calculate the new machine's net present value assuming a 16% discount rate. (For calculation purposes, use 4 decimal places as displayed in the factor table provided and round final answer to 0 decimal place, e.g. 58,971.) Net present value $ (b) Use Excel or a similar spreadsheet application to calculate the new machine's internal rate of return. (Round answer to 2 decimal places, e.g. 1.25%.) % Internal rate of return eTextbook and Media Save for Later Attempts: 0 of 3 used Submit Answer (c) Calculate the new machine's payback period. (Round answer to 2 decimal places, e.g. 1.25.) Payback period years eTextbook and Media Save for Later Attempts: 0 of 3 used Submit Answer APPENDIX 9.1 Present value of S1 received in n periods. Periods 4% 5% 6% 7% 8% 9% 10% 11% 13% 14% 16% 18% 20% 1 2 3 4 5 0.9615 0.9246 0.8890 0.8548 0.8219 0.9524 0.9070 0.8638 0.8227 0.7835 0.9434 0.8900 0.8396 0.7921 0.7473 0.9346 0.8734 0.8163 0.7629 0.7130 0.9259 0.8573 0.7938 0.7350 0.6806 0.9174 0.8417 0.7722 0.7084 0.6499 0.9091 0.8264 0.7513 0.6830 0.6209 0.9009 0.8116 0.7312 0.6587 0.5935 12% 0.8929 0.7972 0.7118 0.6355 0.5674 0.8850 0.7831 0.6931 0.6133 0.5428 0.8772 0.7695 0.6750 0.5921 0.5194 0.8621 0.7432 0.6407 0.5523 0.4761 0.8475 0.7182 0.6086 0.5158 0.4371 0.8333 0.6944 0.5787 0.4823 0.4019 6 7 8 9 10 0.7903 0.7599 0.7307 0.7026 0.6756 0.7462 0.7107 0.6768 0.6146 0.6139 0.7050 0.6651 0.6274 0.5919 0.5584 0.6663 0.6227 0.5820 0.5439 0.5083 0.6302 0.5835 0.5403 0.5002 0.4632 0.5963 0.5470 0.5019 0.4604 0.4224 0.5645 0.5132 0.4665 0.4241 0.3855 0.5346 0.4817 0.4339 0.3909 0.3522 0.5066 0.4523 0.4039 0.3606 0.3220 0.4803 0.4251 0.3762 0.3329 0.2946 0.4556 0.3996 0.3506 0.3075 0.2697 0.4104 0.3538 0.3050 0.2630 0.2267 0.3704 0.3349 0.3139 0.2791 0.2660 -0.2326 0.2255 0.1938 0.1911 0.1615 11 12 13 14 15 0.6496 0.6246 0.6006 0.5775 0.5553 0.5847 0.5568 0.5303 0.5051 0.4810 0.5268 0.4970 0.4688 0.4423 0.4173 0.4751 0.4440 04150 0.3878 0.3624 0.4289 0.3971 0.3677 0.3405 0.3152 0.3875 0.3505 0.3555 0.3186 0.3262 0.2897 0.2992 0.2633 0.2745 0.2394 0.3173 0.2875 0.2607 0.2366 0.1954 0.1619 0.1346 0.2858 0.2567 0.2307 0.2076 0.1685 0.1372 0.1122 0.2575 0.2292 0.2042 0.1821 0.1452 0.1163 0.0935 0.2320 0.2046 0.1807 0.1597 0.1252 0.0985 0.0779 0.2090 0.1827 0.1599 0.1401 0.1079 0.0835 0.0619 16 17 18 19 20 0.5339 0.5134 0.4936 0.4746 0.4564 $1 (1 + i)" 0.4581 0.4363 0.4155 0.3957 0.3769 0.3936 0.3714 0.3503 0.3305 0.3118 0.3387 0.3166 0.2959 0.2765 0.2584 0.2919 0.2519 0.2176 0.1883 0.1631 0.1415 0.1229 0.2703 0.2311 0.1978 0.1696 0.1456 0.1252 0.1078 0.2502 0.2120 0.1799 0.1528 0.1300 0.1108 0.0946 0.2317 0.1945 0.1635 0.1377 0.1161 0.0981 0.0829 0.2145 0.1784 0.1486 0.1240 0.1037 0.0868 0.0728 0.0930 0.0802 0.0691 0.0596 0.0514 0.0708 0.0600 0.0508 0.0431 0,0365 0.0541 0.0451 0.0376 0.0313 0.0261 PV =