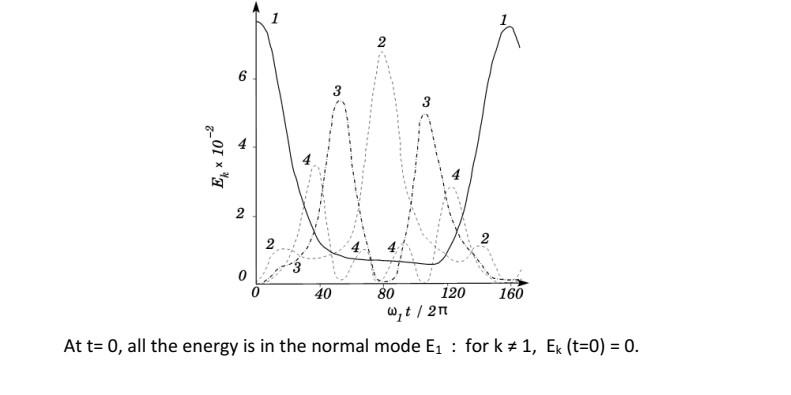
Consider a chain of particles that can interact via nonlinear nearest neighbors -model * = (x. 2x +x__ ) + [ (x.. = x, ) ( , , , ) ] X =X n n n-1 n+1 B-model X = (X+1 2x + X_, ) [(x. x, ) ( x x,- )' ] x B + 'n+1 'n-1 n-1 Xn(t) is the displacement of the nth particle from its equilibrium position. Fixed end point problem: LINEAR NORMAL MODES x (t)=x (t) = ( N kn [case of a=0 or B=0]: Q (1)-( *x. (0) sin ) Ex N n=1 k Normal mode frequency: @= 2 sin 2N Constant of the Motion: Energy of the kth-mode: 1/2 N E = - [Q +Q] =const. Idea: no matter how small the nonlinear coupling terms, for sufficiently large number of modes one would expect the system to reach thermal equilibrium and all states would have the same mean energy ["thermal equilibration"]. The original results from the Fermi et.al. nonlinear numerical experiment in 1955 are shown below for the cubic nonlinearities 8-01 x% 5 2 40 80 120 160 w,t/2n At t= 0, all the energy is in the normal mode E: for k1, Ek (t=0) = 0. The nonlinear coupling excites the other normal modes and things seemed to tend to equilibration of energy among the normal modes. However, around t* = 160, all the energy seems to have returned back just to the k = 1 mode. The idea is to study this phenomenon on nonlinear recurrence. OUTLINE of PROBLEM (a) Choose N = 8, =0= Put all the energy in k = 1 mode. Plot the energies Ek(t) for all the normal modes. Now put 75% energy in k = 1 mode, and 25% into k = 3 mode. Plot the energies Ex(t) for all the normal modes. (b) Choose N = 8, #0 e.g., p=0.3, 1.0, 3.0 outlined in (a) Repeat the simulations (c) Choose N= 32, B #0 e.g., p=0.3, 1.0, 3.0 Repeat the simulations outlined in (a) (d) Choose N= 32, #0 : e.g., p=0.003, p=0.03 Repeat the simulations outlined in (a)