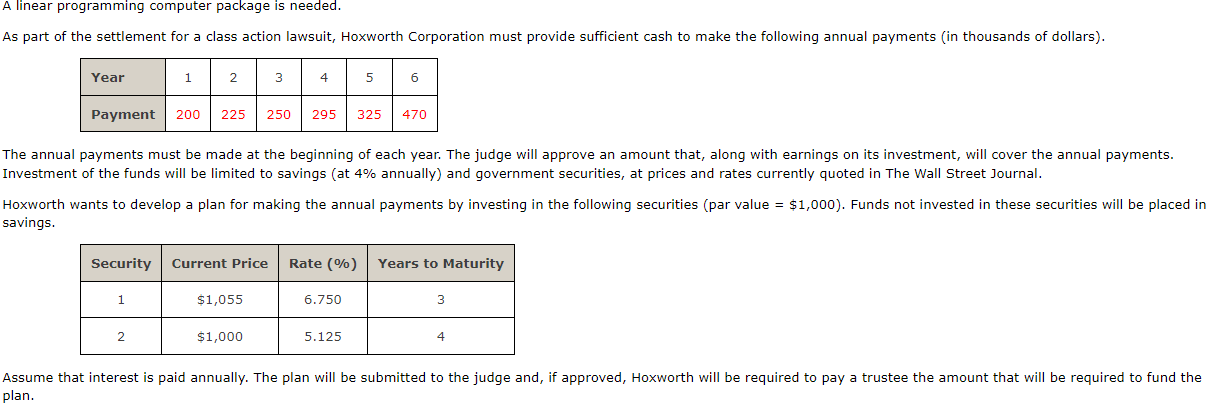

The annual payments must be made at the beginning of each year. The judge will approve an amount that, along with earnings on its investment, will cover the annual payments. Investment of the funds will be limited to savings (at 4% annually) and government securities, at prices and rates currently quoted in The Wall Street Journal. Hoxworth wants to develop a plan for making the annual payments by investing in the following securities (par value =$1,000 ). Funds not invested in these securities will be placed savings. (a) Use linear programming to find the minimum cash settlement necessary (in $ ) to fund the annual payments. (Round your answer to the nearest dollar.) $ (b) Use the dual value to determine how much more (in \$) Hoxworth should be willing to pay now to reduce the payment at the beginning of year 6 to $400,000. (Round your answer to the nearest dollar.) $ (c) Use the dual value to determine how much more (in \$) Hoxworth should be willing to pay to reduce the year 1 payment to $150,000. (Round your answer to the nearest dollar.) $ (d) Suppose that the annual payments are to be made at the end of each year. Reformulate the model to accommodate this change. How much would Hoxworth save (in \$) if this change could be negotiated? (Round your answer to the nearest dollar.) $ The annual payments must be made at the beginning of each year. The judge will approve an amount that, along with earnings on its investment, will cover the annual payments. Investment of the funds will be limited to savings (at 4% annually) and government securities, at prices and rates currently quoted in The Wall Street Journal. Hoxworth wants to develop a plan for making the annual payments by investing in the following securities (par value =$1,000 ). Funds not invested in these securities will be placed savings. (a) Use linear programming to find the minimum cash settlement necessary (in $ ) to fund the annual payments. (Round your answer to the nearest dollar.) $ (b) Use the dual value to determine how much more (in \$) Hoxworth should be willing to pay now to reduce the payment at the beginning of year 6 to $400,000. (Round your answer to the nearest dollar.) $ (c) Use the dual value to determine how much more (in \$) Hoxworth should be willing to pay to reduce the year 1 payment to $150,000. (Round your answer to the nearest dollar.) $ (d) Suppose that the annual payments are to be made at the end of each year. Reformulate the model to accommodate this change. How much would Hoxworth save (in \$) if this change could be negotiated? (Round your answer to the nearest dollar.) $








