Question
the book is intermolecular and suface forces 3rd ed and at page20 1.4 problem Two atoms interact via a Lennard-Jones potential, Eq. (1.7), with interaction
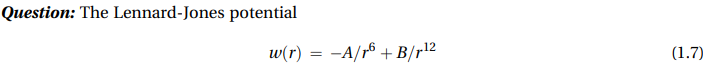
the book is "intermolecular and suface forces 3rd ed" and at page20 1.4 problem
Two atoms interact via a Lennard-Jones potential, Eq. (1.7), with interaction constants A 10^-77J m^6 and B 10^-134J m^12 (as in the Worked Example 1.2). Consider two such atoms in contact?that is, sitting in their potential energy minimum at a mean separation re from each other, when they start being pulled apart by a constant externally applied force of F0 10 pN. Plot the net force F(r) and energy w(r) experienced by each atom as a function of the interatomic separation, r. Explain how each plot predicts the same new equilibrium separation, re. Determine this new value, and calculate the ratio of re to the equilibrium spacing at F = 0?that is, under no external force. By trial and error, graphically determine what force will just cause the two atoms to fly apart to infinity. Again plot the net force and energy functions, F(r) and w (r), for this case, and briefly explain how each determines the adhesion or pull-off force F0 and the "metastable" separation, re = rs, just before the two atoms fly apart. From your graph, determine the pull-off force and the ratio of rs to the equilibrium spacing re at F 0 (give your results with your measuring error) and compare both values to the theoretical values. Your results are strictly valid only at zero temperature (T = 0; K = -273C). Discuss qualitatively whether and how your answers will be different in practice? in other words, in a genuine laboratory experiment carried out at room temperature and over a finite time. [Suggestion: Choose your axes carefully so that you use the maximum space for displaying the essential features of your plots (suggested range for r: 0.25 to 0.60 nm).

Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


