The continuous function f f is defined for −4≤x≤4 − 4 ≤ x ≤ 4 . The graph of f f , shown above, consists of two line segments and portions of three parabolas. The graph has horizontal tangents at x=−12, x=12 x = − 1 2 , x = 1 2 and x=52 x = 5 2 . It is known that f(x)=−x2+5x−4 f ( x ) = − x 2 + 5 x − 4 for 1≤x≤4 1 ≤ x ≤ 4 . The areas of regions A and B bounded by the graph of f f and the x− x − axis are 3 and 5, respectively. Let g g be the function defined by g(x)=∫x−4f(t)dt g ( x ) = ∫ − 4 x f ( t ) d t .

(a) Find g(0) and g(4).

(b) Find the absolute minimum value of g on the closed interval [-4,4]. Justify your answer.

(c) Find all interval for which the graph of g is concave down. Give a reason for your answer.

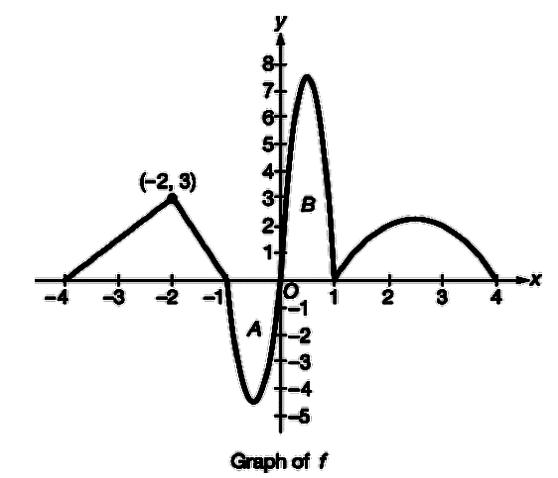
5+ (-2, 3) 3 B 2- 1- -2 2 A Graph of f