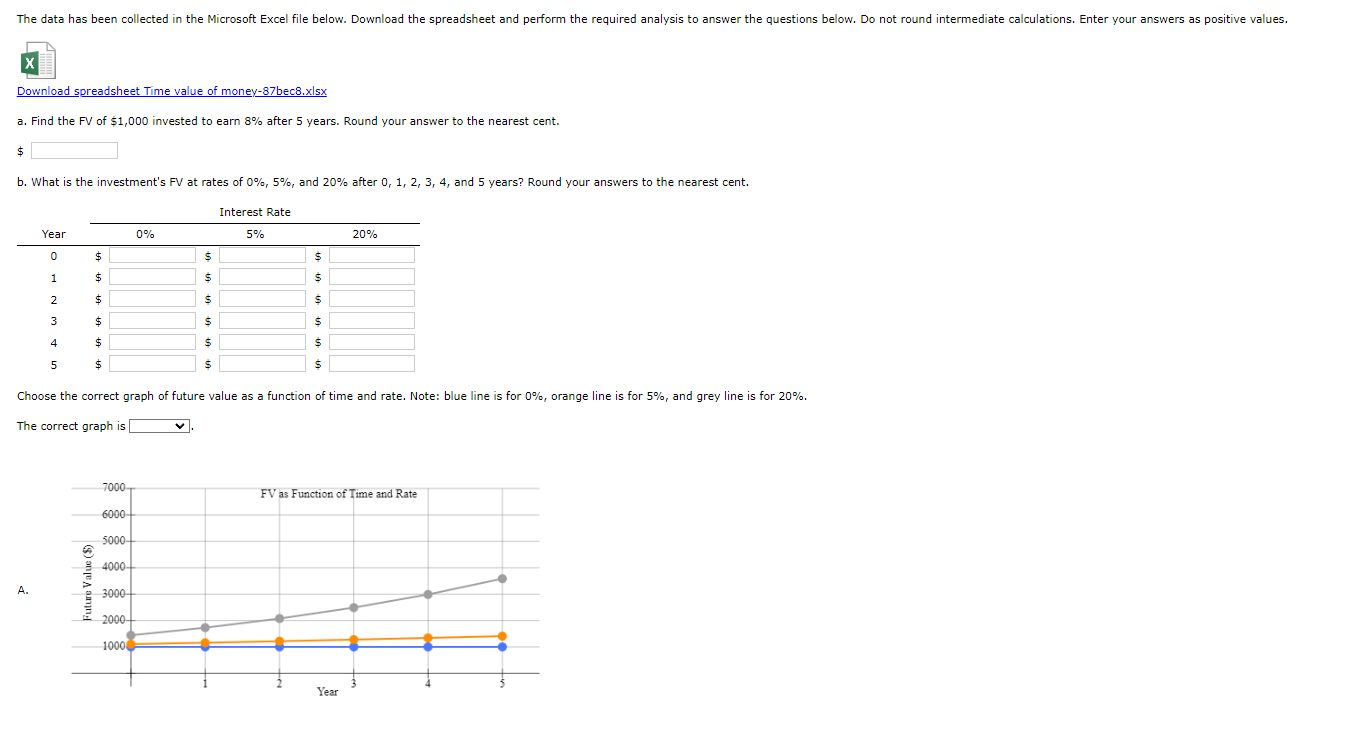
The data has been collected in the Microsoft Excel file below. Download the spreadsheet and perform the required analysis to answer the questions below. Do not round intermediate calculations. Enter your answers as positive values. Download spreadsheet Time value of money-87bec8.xlsx a. Find the FV of $1,000 invested to earn 8% after 5 years. Round your answer to the nearest cent. $ b. What is the investment's FV at rates of 0%, 5%, and 20% after 0, 1, 2, 3, 4, and 5 years? Round your answers to the nearest cent. Interest Rate Year 0% 5% 20% 0 $ $ s 1 $ $ $ 2 $ $ $ 3 $ $ $ 4 $ $ $ $ 5 $ Choose the correct graph of future value as a function of time and rate. Note: blue line is for 0%, orange line is for 5%, and grey line is for 20%. The correct graph is 7000 FV as Function of Time and Rate 6000 5000 4000 A. 3000 2000 1000 Year Time value of money a. Finding FV Investment (PV) Interest rate (1) Number of years (N) Future value (FV) $1,000 8% 5 Formula #N/A Interest Rate (B5) 0% 5% 20% b. Creating a table with FVs at various interest rates and time periods using Data Table Year (B6) Interest Rate (B5) 0% 5% 20% 0 1 2 3 4 5 Formulas Year (B6) #N/A 0 1 1 2 3 4 4 5. #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A Creating a graph with years on the horizontal axis and FV on the vertical axis c. Finding PV Future value (FV) Discount rate (1) Number of years (N) Present value (PV) $1,000 8% 5 Formulas #N/A d. Finding the rate of return provided by the security Cost of security (PV) $1,000 Future value of security (FV) $4,000 Number of years (N) 5 Rate of return (1) #N/A e. Calculating the number of years required to double the population Current population in millions (PV) 36 Growth rate (1) 2% Doubled population in millions (FV) #N/A Number of years required to double (N) #N/A f. Finding the PV and FV of an ordinary annuity Annuity (PMT) $1,000 Interest rate (1) 10% Number of years (N) 5 Present value of ordinary annuity (PV) #N/A Future value of ordinary annuity (FV) #N/A g. Recalculating the PV and FV for part f if the annuity is an annuity due Present value of annuity due (PV) '#N/A Future value of annuity due (FV) '#N/A h. Recalculating the PV and the FV for parts a and c if the interest rate is semiannually compounded Future value (FV) '#N/A Present value (PV) #N/A i. Finding the annual payments for an ordinary annuity and an annuity due Present value (PV) $1,000 Discount rate (1) 7% Number of years (N) 10 Annual payment for ordinary annuity (PMT1) #N/A Annual payment for annuity due (PMT2) #N/A j. Finding the PV and the FV of an investment that makes the following end-of-year payments Year Payment 1 $200 2 $400 3 $600 Interest rate (1) Present value of investment (PV) Future value of investment (FV) 7% #N/A #N/A k. Five banks offer the same nominal rate on deposits, but A pays interest annually, B pays semiannually, C pays quarterly, D pays monthly, and E pays daily. (1) Calculating the effective annual rate for each bank and the future values of the deposit at the end of 1 year and 2 years Nominal rate (IOM) 6% Deposit (PV) $5,500 Number of days per year 365 Formulas B D E A EAR EAR #N/A FV after 1 year FV after 1 year #N/A FV after 2 years FV after 2 years #N/A B #N/A #N/A #N/A #N/A #N/A #N/A D #N/A #N/A #N/A (2) Calculating the nominal rates that will cause all of the banks to provide the same effective annual rate as Bank A B D E Nominal rate (INOM) B #N/A #N/A D #N/A E #N/A Nominal rate (INOM) (3) Calculating the amount of payment to be made annually for A, semiannually for B, quarterly for C, monthly for D, and daily for E Needed amount (FV) $5,500 Number of years (N) 1 A B D E A #N/A B #N/A #N/A D #N/A Payment (PMT) Payment (PMT) 1. Setting up the amortization schedule Original amount of mortgage (PV) Interest rate (0) Term to maturity, years (N) $14.000 7% 4 Formula #N/A Annual payment (PMT) Formulas Beginning Balance Payment Repayment of Principal Interest Ending Balance Payment #N/A Year 1 2 3 4 Year 1 2 3 4 Beginning Balance #N/A #N/A #N/A #N/A Interest #N/A #N/A #N/A #N/A Repayment of Principal #N/A #N/A #N/A #N/A #N/A #N/A #N/A Creating a graph that shows how the payments are divided between interest and principal repayment over time The data has been collected in the Microsoft Excel file below. Download the spreadsheet and perform the required analysis to answer the questions below. Do not round intermediate calculations. Enter your answers as positive values. Download spreadsheet Time value of money-87bec8.xlsx a. Find the FV of $1,000 invested to earn 8% after 5 years. Round your answer to the nearest cent. $ b. What is the investment's FV at rates of 0%, 5%, and 20% after 0, 1, 2, 3, 4, and 5 years? Round your answers to the nearest cent. Interest Rate Year 0% 5% 20% 0 $ $ s 1 $ $ $ 2 $ $ $ 3 $ $ $ 4 $ $ $ $ 5 $ Choose the correct graph of future value as a function of time and rate. Note: blue line is for 0%, orange line is for 5%, and grey line is for 20%. The correct graph is 7000 FV as Function of Time and Rate 6000 5000 4000 A. 3000 2000 1000 Year Time value of money a. Finding FV Investment (PV) Interest rate (1) Number of years (N) Future value (FV) $1,000 8% 5 Formula #N/A Interest Rate (B5) 0% 5% 20% b. Creating a table with FVs at various interest rates and time periods using Data Table Year (B6) Interest Rate (B5) 0% 5% 20% 0 1 2 3 4 5 Formulas Year (B6) #N/A 0 1 1 2 3 4 4 5. #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A #N/A Creating a graph with years on the horizontal axis and FV on the vertical axis c. Finding PV Future value (FV) Discount rate (1) Number of years (N) Present value (PV) $1,000 8% 5 Formulas #N/A d. Finding the rate of return provided by the security Cost of security (PV) $1,000 Future value of security (FV) $4,000 Number of years (N) 5 Rate of return (1) #N/A e. Calculating the number of years required to double the population Current population in millions (PV) 36 Growth rate (1) 2% Doubled population in millions (FV) #N/A Number of years required to double (N) #N/A f. Finding the PV and FV of an ordinary annuity Annuity (PMT) $1,000 Interest rate (1) 10% Number of years (N) 5 Present value of ordinary annuity (PV) #N/A Future value of ordinary annuity (FV) #N/A g. Recalculating the PV and FV for part f if the annuity is an annuity due Present value of annuity due (PV) '#N/A Future value of annuity due (FV) '#N/A h. Recalculating the PV and the FV for parts a and c if the interest rate is semiannually compounded Future value (FV) '#N/A Present value (PV) #N/A i. Finding the annual payments for an ordinary annuity and an annuity due Present value (PV) $1,000 Discount rate (1) 7% Number of years (N) 10 Annual payment for ordinary annuity (PMT1) #N/A Annual payment for annuity due (PMT2) #N/A j. Finding the PV and the FV of an investment that makes the following end-of-year payments Year Payment 1 $200 2 $400 3 $600 Interest rate (1) Present value of investment (PV) Future value of investment (FV) 7% #N/A #N/A k. Five banks offer the same nominal rate on deposits, but A pays interest annually, B pays semiannually, C pays quarterly, D pays monthly, and E pays daily. (1) Calculating the effective annual rate for each bank and the future values of the deposit at the end of 1 year and 2 years Nominal rate (IOM) 6% Deposit (PV) $5,500 Number of days per year 365 Formulas B D E A EAR EAR #N/A FV after 1 year FV after 1 year #N/A FV after 2 years FV after 2 years #N/A B #N/A #N/A #N/A #N/A #N/A #N/A D #N/A #N/A #N/A (2) Calculating the nominal rates that will cause all of the banks to provide the same effective annual rate as Bank A B D E Nominal rate (INOM) B #N/A #N/A D #N/A E #N/A Nominal rate (INOM) (3) Calculating the amount of payment to be made annually for A, semiannually for B, quarterly for C, monthly for D, and daily for E Needed amount (FV) $5,500 Number of years (N) 1 A B D E A #N/A B #N/A #N/A D #N/A Payment (PMT) Payment (PMT) 1. Setting up the amortization schedule Original amount of mortgage (PV) Interest rate (0) Term to maturity, years (N) $14.000 7% 4 Formula #N/A Annual payment (PMT) Formulas Beginning Balance Payment Repayment of Principal Interest Ending Balance Payment #N/A Year 1 2 3 4 Year 1 2 3 4 Beginning Balance #N/A #N/A #N/A #N/A Interest #N/A #N/A #N/A #N/A Repayment of Principal #N/A #N/A #N/A #N/A #N/A #N/A #N/A Creating a graph that shows how the payments are divided between interest and principal repayment over time