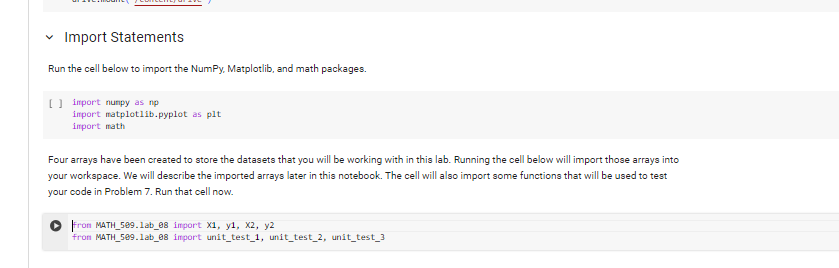
The data that is needed is stored in arrays X2 and y2 previously ran earlier in the notebook.

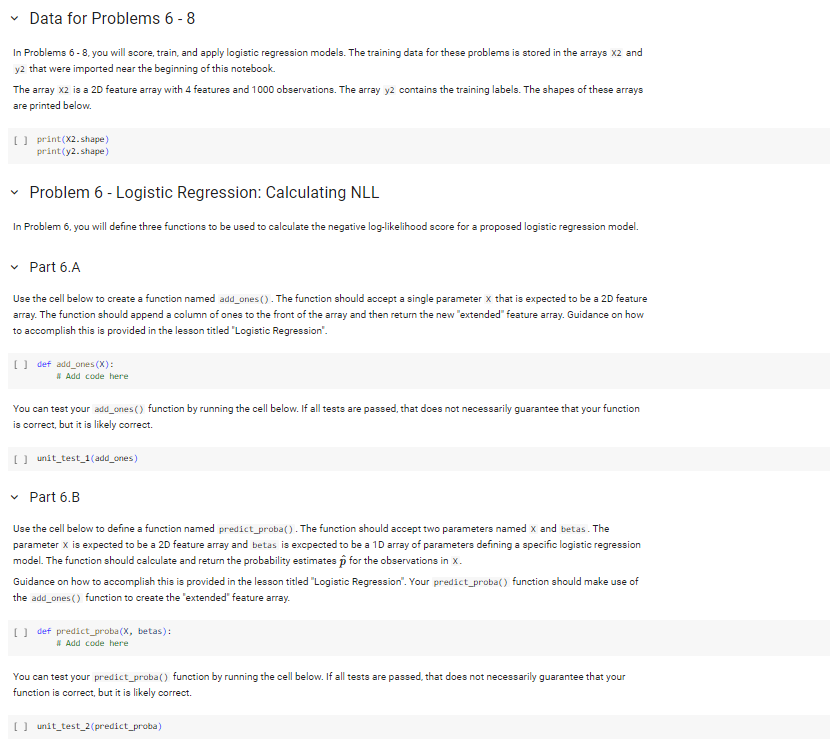
Import Statements Run the cell below to import the NumPy, Matplotlib, and math packages. [ ] import numpy as np import matplotilib.pyplot as plt import math Four arrays have been created to store the datasets that you will be working with in this lab. Running the cell below will import those arrays into your workspace. We will describe the imported arrays later in this notebook. The cell will also import some functions that will be used to test your code in Problem 7. Run that cell now. fron MATH_599.1ab_08 import x1,y1,x2,y2 fron MATH_599.1ab_68 import unit_test_1, unit_test_2, unit_test_3 In Problems 68, you will score, train, and apply logistic regression models. The training data for these problems is stored in the arrays X2 and y2 that were imported near the beginning of this notebook. The array X2 is a 2D feature array with 4 features and 1000 observations. The array y2 contains the training labels. The shapes of these arrays are printed below. [ ] print(X2.shape) print(y2.shape) Problem 6 - Logistic Regression: Calculating NLL In Problem 6, you will define three functions to be used to calculate the negative log-likelihood score for a proposed logistic regression model. Part 6.A Use the cell below to create a function named add_ones(). The function should accept a single parameter x that is expected to be a 2D feature array. The function should append a column of ones to the front of the array and then return the new "extended" feature array. Guidance on how to accomplish this is provided in the lesson titled "Logistic Regression". [ ] def add_ones (X) : A Add code here You can test your add_ones() function by running the cell below. If all tests are passed, that does not necessarily guarantee that your function is correct, but it is likely correct. [ ] unit_test_1(add_ones) Part 6.B Use the cell below to define a function named predict_proba(). The function should accept two parameters named x and betas. The parameter x is expected to be a 2D feature array and betas is excpected to be a 1D array of parameters defining a specific logistic regression model. The function should calculate and return the probability estimates p^ for the observations in x. Guidance on how to accomplish this is provided in the lesson titled "Logistic Regression". Your predict_proba() function should make use of the add_ones() function to create the "extended" feature array. [ ] def predict_proba( X, betas): I Add code here You can test your predict_proba() function by running the cell below. If all tests are passed, that does not necessarily guarantee that your function is correct, but it is likely correct. Use the cell below the define a function named calculate_NLL (). The function should accept three parameters named x, y, and betas. The parameter x is expected to be a 2D feature array, y is expected to be a 1D label array, and betas is expected to be a 1D array of parameters defining a specific logistic regression model. The function should use predict_proba() to generate probability estimates for the observations contained in x and y and should then calculate and return the NLL score for the model given by betas. Guidance on how to accomplish this is provided in the lesson titled "Training a Logistic Regression Model". [ ] def calculate_NLL (x,y, betas): I Add code here You can test your calculate_NLL() function by running the cell below. If all tests are passed, that does not necessarily guarantee that your function is correct, but it is likely correct. [ ] unit_test_3(calculate_NLL) Part 6.D You will now used your calculate_NLL() function to score two logistic regression models. The cell below contains definitions for two parameter arrays betas1 and betas 2 . These arrays represent the two models shown below. p^=(2X(1)3X(2)+2X(3)+3X(4))p^=(5+X(1)4X(2)+3X(3)+5X(4)) Use your calculate_NLL() function to score each of these models using the training data stored in X2 and y2. Print the NLL scores for both models, rounded to 2 decimal places. []betas1=[2,1,3,2,3]betas2=[5,1,4,3,5] "I Add code here