the differential equation 4x () = 7 if x = 10 when t = 0: t+ 100 t+ 10...

Transcribed Image Text:

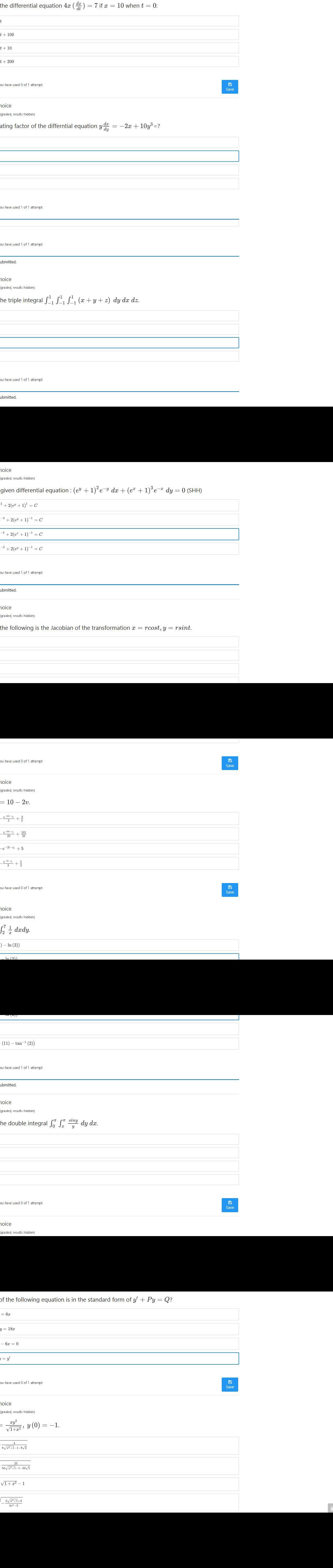
the differential equation 4x () = 7 if x = 10 when t = 0: t+ 100 t+ 10 t+ 200 ou have used 0 of 1 attempt Save noice graded, results hidden) ating factor of the differntial equation y = -2x + 10y3 =? dy ou have used 1 of 1 attempt ou have used 1 of 1 attempt ubmitted. noice (graded, results hidden) he triple integral SLL (x+ y+ z) dy dæ dz. ou have used 1 of 1 attempt ubmitted. noice graded, results hidden) given differential equation : (ev +1)'e-y dx + (e" + 1)°e- dy = 0 (SHH) + 2(e +1)' = C -3 + 2(e + 1) = C -2 + 2(e* + 1)-1 = C -2 + 2(ev + 1)-1 = C ou have used 1 of 1 attempt ubmitted. noice graded, results hidden) the following is the Jacobian of the transformation x = rcost, y = rsint. ou have used 0 of 1 attempt Save noice (graded, results hidden) = 10 – 2v. -e-2t-ci + 5 ou have used 0 of 1 attempt Save noice (graded, results hidden) dædy. ) - In (2)) In (211 (11) – tan-1 (2)) ou have used 1 of 1 attempt ubmitted. noice (graded, results hidden) he double integral Jo S siny dy da. ou have used 0 of 1 attempt Save noice (graded, results hidden) of the following equation is in the standard form of y + Py = Q? = 6z = 187 - 6z = 0 ou have used 0 of 1 attempt Save noice graded, results hidden) xy VIta? Y (0) = -1. 87+1-1-8V2 25 50 V +1-1-50/5 VI+ a? - 1 2+1+3 4-5 0.00 2:15 98% 4 KB/S 14. Solve the differential equation 4x () = 7 if x = 10 when dx dt t = 0: 2x2 = 7t 2x2 = 7t + 100 2x2 7t + 10 2x2 = 7t + 200 Submit You have used 0 of 1 attempt Save Multiple Choice 1 point possible (graded, results hidden) 20. Integrating factor of the differntial equation dx Y Y dy = -2x + 10y=? y +1 y +3 Submit You have used 0 of 1 attempt Save Multiple Choice 1 point possible (graded, results hidden) Evaluate the triple integral 1 1 1 Si SI S5 (x + y+ z) dy dx d 1 1 2 6. Submit You have used 0 of 1 attempt Save Multiple Choice 1 point possible (graded, results hidden) Solve the given differential equation : (ev + 1)?ey dx + (e" +1)°e (SHH) 1)*e= (e" + 1)² + 2(ev + 1)' = C (e" + 1)-³ + 2(ev +1)-1 = C (ey + 1)-2 + 2(e + 1)-1 = C (e* + 1)¯² + 2(ev + 1)-1 = C Submit You have used 0 of 1 attempt Save Multiple Choice 1 point possible (graded, results hidden) Which of the following is the Jacobian of the transformation rcost, y = rsint. 3r-2 3r 2r-3 Submit You have used 0 of 1 attempt Save Multiple Choice 1 point possible (graded, results hidden) dv Solve dt 10 – 2v. -25t-C1 v (t) 3 + -25t-C1 e 101 v (t) : 25 25 -2t-C1 +5 v (t) -e -3t-C1 e v (t) = + 3 3 Submit You have used 0 of 1 attempt Save Multiple Choice 1 point possible (graded, results hidden) xy³ Solve y y (0) = –1. /1+x² 4 y = 8Vx2+1–1-8/2 25 y = 50vx2+1-1-50/5 1 V1 + x2 – 1 2y? 2Vx2+1+3 y = 4x2 -5 Submit You have used 0 of 1 attempt Save Multiple Choice 1 point possible (graded, results hidden) Evaluate the double integral T siny dy dx. -2 1 Submit You have used 0 of 1 attempt Save Multiple Choice 1 point possible (graded, results hidden) 9. Which of the following equation is in the standard form of y + Py = Q? y – y = 6x - 9. 3y – y = 18x 3 y – y – 6x = 0 - - 3 2.

Answer rating: 100% (QA)

Detailed View the full answer