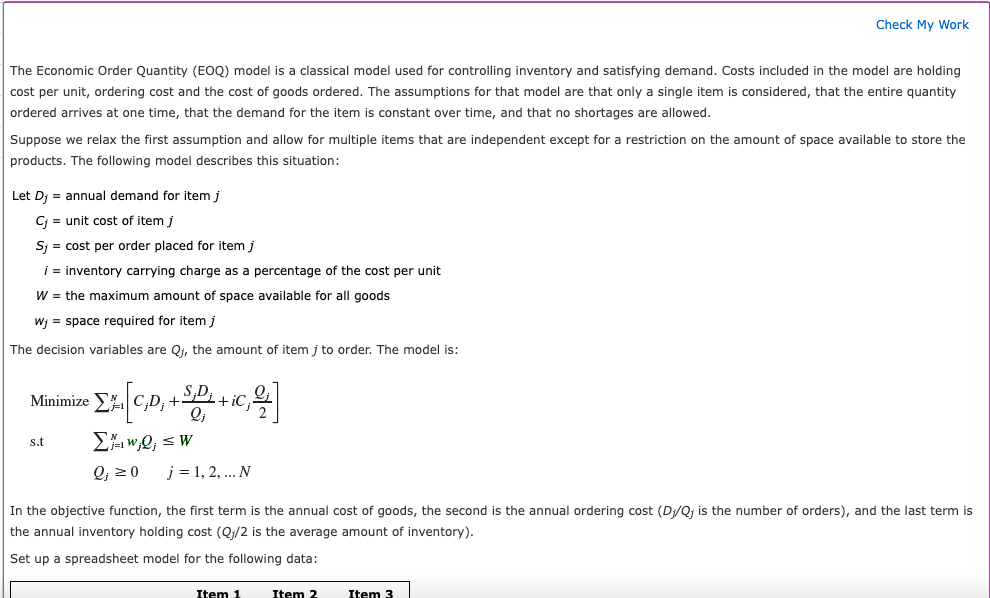
The Economic Order Quantity (EOQ) model is a classical model used for controlling inventory and satisfying demand. Costs included in the model are holding products. The following model describes this situation: Let Dj= annual demand for item j Cj= unit cost of item j Sj= cost per order placed for item j i= inventory carrying charge as a percentage of the cost per unit W= the maximum amount of space available for all goods wj= space required for item j The decision variables are Qj, the amount of item j to order. The model is: Minimizes.tj=1N[CjDj+QjSjDj+iCj2Qj]j=1NwjQjWQj0j=1,2,N In the objective function, the first term is the annual cost of goods, the second is the annual ordering cost ( Dj/Qj is the number of and is the annual inventory holding cost (Qj/2 is the average amount of inventory). Set up a spreadsheet model for the following data: the annual inventory holding cost (Qj/2 is the average amount of inventory). Set up a spreadsheet model for the following data: W=5,000i=0.3 Solve the problem using Excel Solver. Hint: You will need to start with decision variable values that are greater than 0 for Solver to find a solution. If required, round your answers to two decimal places. Optimal Solution: Q1=Q2=Q3= If required, round your answer to the nearest dollar. Do not round intermediate calculations. Total cost =$ 0= Icon Key The Economic Order Quantity (EOQ) model is a classical model used for controlling inventory and satisfying demand. Costs included in the model are holding products. The following model describes this situation: Let Dj= annual demand for item j Cj= unit cost of item j Sj= cost per order placed for item j i= inventory carrying charge as a percentage of the cost per unit W= the maximum amount of space available for all goods wj= space required for item j The decision variables are Qj, the amount of item j to order. The model is: Minimizes.tj=1N[CjDj+QjSjDj+iCj2Qj]j=1NwjQjWQj0j=1,2,N In the objective function, the first term is the annual cost of goods, the second is the annual ordering cost ( Dj/Qj is the number of and is the annual inventory holding cost (Qj/2 is the average amount of inventory). Set up a spreadsheet model for the following data: the annual inventory holding cost (Qj/2 is the average amount of inventory). Set up a spreadsheet model for the following data: W=5,000i=0.3 Solve the problem using Excel Solver. Hint: You will need to start with decision variable values that are greater than 0 for Solver to find a solution. If required, round your answers to two decimal places. Optimal Solution: Q1=Q2=Q3= If required, round your answer to the nearest dollar. Do not round intermediate calculations. Total cost =$ 0= Icon Key