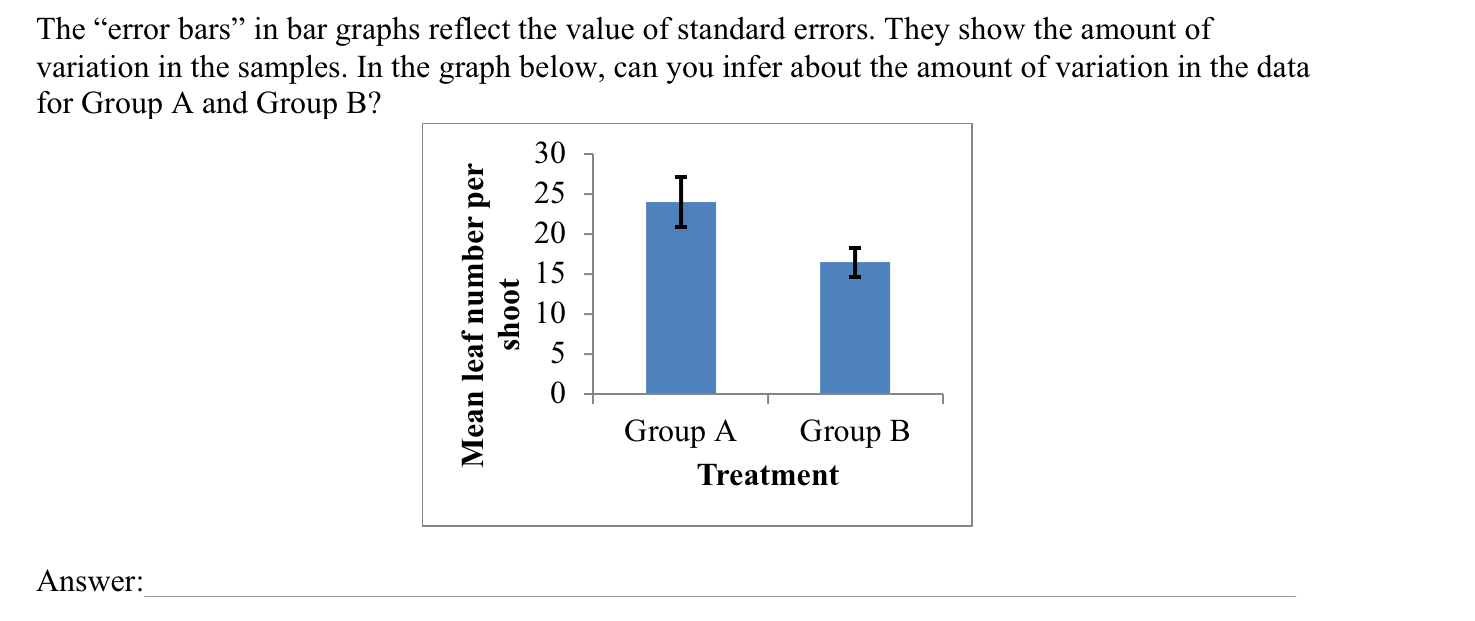
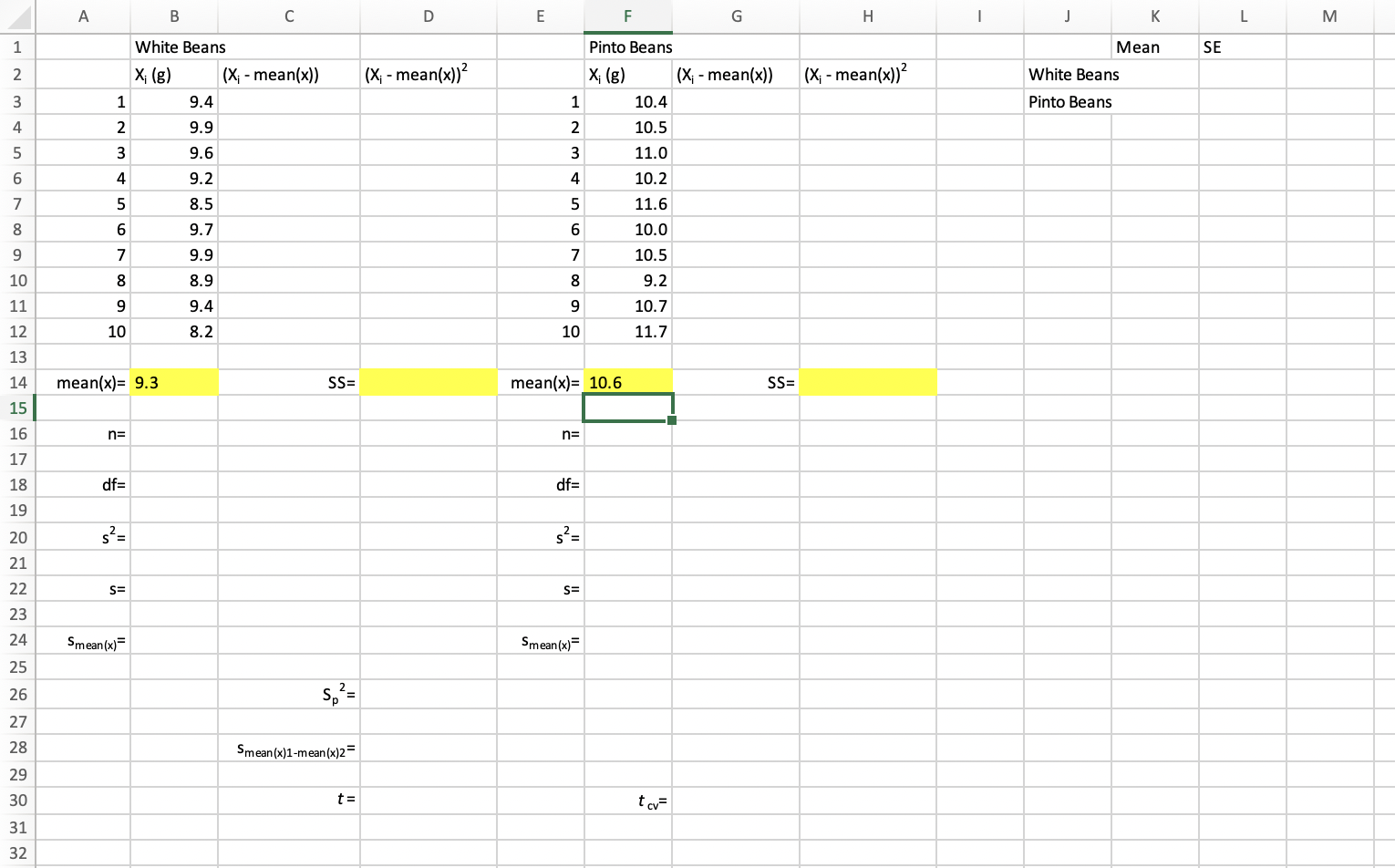
The "error bars" in bar graphs reflect the value of standard errors. They show the amount of variation in the samples. In the graph below, can you infer about the amount of variation in the data for Group A and Group B? Mean leaf number per shoot 30 25 20 15 Group A Group B Treatment Answer: Using your data, perform the t-test (an unpaired t-test): 1. Obtain a quantity called pooled variance (SP2): Sp = (SS1 SS2)/ (df1 + df2) SS1 & SS2 refer to the sum of squares of each sample (white beans and pinto beans), and dfi & df2 represent the number of degrees of freedom in each sample. Pooled variance is a collective measure of the variation in both samples. Degrees of freedom in each sample (df1 + df2) are simply defined as n-1, where n represents the size of sample 1 and sample 2. Note: degrees of freedom are NOT always defined as (n-1). 2. Using the pooled variance (SR22) value you just calculated, obtain standard error of the difference between means, (Smean(x)1-mean(x)2), of pinto and white beans: = Smean(x)1-mean(x)2 (SR/n1 + Sp/n2) 0.5 Answer: *The standard error of the difference between sample means is a different quantity than the standard error of the mean you obtained earlier (step 7 on p. 3). 3. We use Smean(x)1-mean(x)2 in the t-test. The standard error of the difference in means is the denominator in the t-test equation. Using your values, calculate the value of t. t = (mean(x)1 mean(x)2) Smean(x)1-mean(x)2 Answer: t= Note that the t-test incorporates information on both sample means and collective variation in the two samples. Large values of t indicate that means are significantly different; smaller values indicate that they are not. As a general rule, the means of samples are more likely to be significantly different if i. the means are very different, and, ii. there is little variation within each sample. The lower the variation within each group, the greater the likelihood a significance difference exists between the two groups if the means are different. The value of t is large when the numerator is large (a large difference between X 1 and X 2) and/or when the denominator (Smean(x)1-mean(x)2) value is small. If Smean(x)1-mean(x)2 is a large value, what does it indicate about variation in the two samples? Answer: General rule of thumb: large variation in the data is the enemy of statistical significance. More variation results in a larger denominator value in the t-test, yielding lower values of t. Recall from freshman biology that a null hypothesis has a companion alternate hypothesis. Write the alternate below: HA: We test the null hypothesis using the statistical analysis, in this case we use a t-test. If we find that the data DO NOT support the null, then the null is rejected. If the data DO support the null, then the null is NOT rejected. A H | J K Mean White Beans Pinto Beans B White Beans D E F Pinto Beans X; (g) (X; - mean(x)) (X; -mean(x)) X; (g) (X; - mean(x)) (X; - mean(x)) 9.4 9.9 2 NH 1 10.4 10.5 9.6 3 11.0 9.2 4 10.2 8.5 5 5 11.6 9.7 6 10.0 9.9 7 10.5 8.9 8 9.2 9.4 9 10.7 8.2 10 11.7 1234567890 1234567 8 9 GENEN22292222222222 10 11 12 13 14 mean(x)= 9.3 15 16 n= 17 18 #P df= 19 20 s = 21 S= 23 24 Smean(x) 25 26 27 28 30 31 32 SS= mean(x)= 10.6 Smean(x)1-mean(x)2= t= n= df= s = S= Smean(x) tcv= SS= SE L M