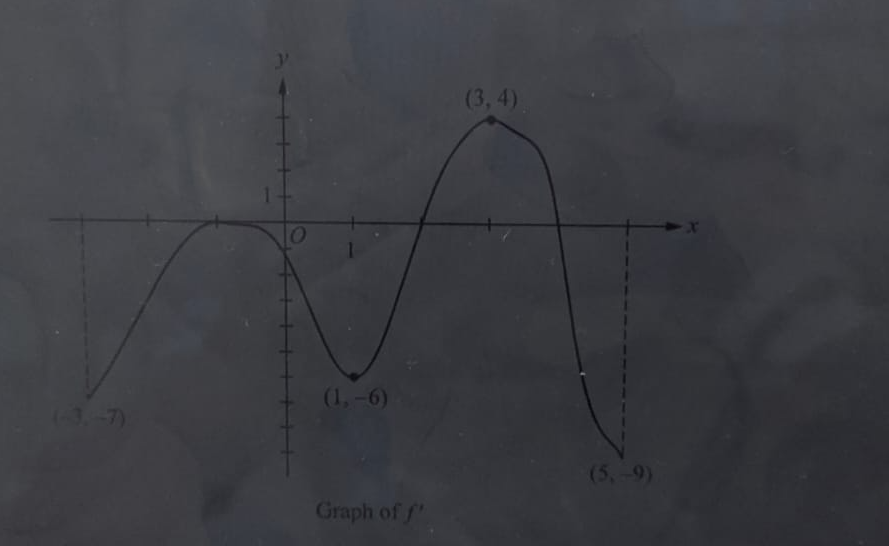
The figure above shows the graph of f', the derivative of a twice-differentiable function f, on the closed interval -3 x 5. The graph of f' has horizontal tangent lines at x = 1, x = 1, and x = 3. The areas of the regions bounded by the x-axis and the graph of f' on the intervals [-3,-1], [-1, 2], [2, 4], and [4, 5] are 6, 8, 5.6, and 6, respectively. The function f is defined for all real numbers and satisfies f(3) = 10 and f(5) = 7. (a) Find the x-coordinate of each critical point of f on the open interval -3 < x < 5. (b) Identify the critical point from part (a) which corresponds to a relative minimum of f. Give a reason for your answer. (c) Find the value off at the x-coordinate identified in part (b). Show the computations that lead to your answer. (d) Find the absolute minimum value of fon -3 x 5. Justify your answer. (e) On what open intervals is f both decreasing and concave down? Give a reason for your answer. (f) Explain why there must be a value of d, for 3 < d < 5, such that f(d) = 8.5. (1,-6) Graph of f (3,4) (5,-9)