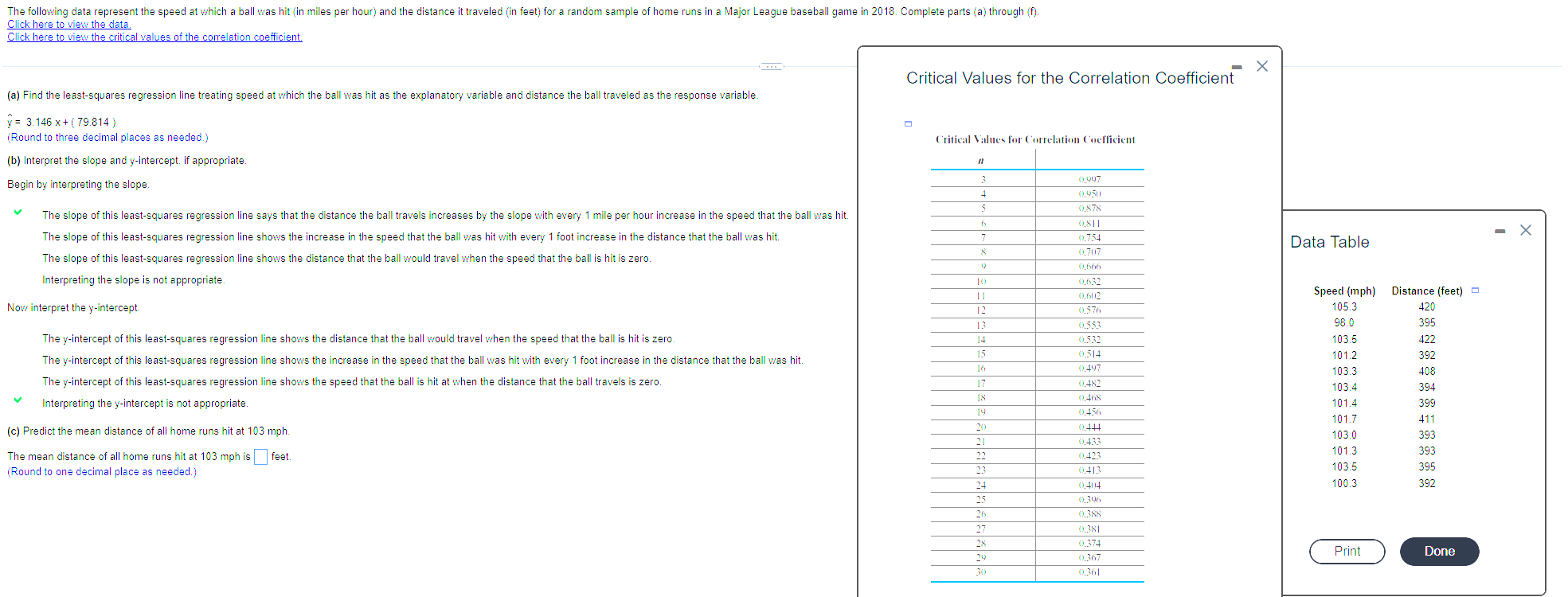
The following data represent the speed at which a ball was hit (in miles per hour) and the distance it traveled (in feet) for a random sample of home runs in a Major League baseball game in 2018. Complete parts (a) through (f). Click here to view the critical values of the correlation coefficient. Click here to view the data. (a) Find the least-squares regression line treating speed at which the ball was hit as the explanatory variable and distance the ball traveled as the response variable. y= 3.146 x + (79.814) (Round to three decimal places as needed.) (b) Interpret the slope and y-intercept. if appropriate. Critical Values for the Correlation Coefficient Critical Values for Correlation Coefficient " 0,997 Begin by interpreting the slope. 4 0,950 5 0.878 The slope of this least-squares regression line says that the distance the ball travels increases by the slope with every 1 mile per hour increase in the speed that the ball was hit. The slope of this least-squares regression line shows the increase in the speed that the ball was hit with every 1 foot increase in the distance that the ball was hit. f 0.811 7 0.754 Data Table 8 0,707 The slope of this least-squares regression line shows the distance that the ball would travel when the speed that the ball is hit is zero. Interpreting the slope is not appropriate. Now interpret the y-intercept. 9 0,666 10 0.632 11 0,602 Speed (mph) Distance (feet) 12 0.576 105.3 420 13 0.553 98.0 395 The y-intercept of this least-squares regression line shows the distance that the ball would travel when the speed that the ball is hit is zero. 14 0.532 103.5 422 15 0.514 101.2 392 The y-intercept of this least-squares regression line shows the increase in the speed that the ball was hit with every 1 foot increase in the distance that the ball was hit. The y-intercept of this least-squares regression line shows the speed that the ball is hit at when the distance that the ball travels is zero. Interpreting the y-intercept is not appropriate. (c) Predict the mean distance of all home runs hit at 103 mph. 16 0.497 103.3 408 17 0.482 103.4 394 18 0,468 101.4 399 19 0.456 101.7 411 20 0.444 103.0 393 21 0.433 101.3 393 The mean distance of all home runs hit at 103 mph is (Round to one decimal place as needed.) feet. 22 0.423 23 0.413 103.5 395 24 0,404 100.3 392 25 0.396 26 0.388 27 0.381 28 0.374 Print Done 29 0.367 30 0.361