Question

1 Approved Answer

Posted on Jul 15, 2024

The following LP formulation represents a transportation problem where raw material (in tons) is transported from Supplier i. i={1,2,3} to Plant j.J={1,2,3). The problem is

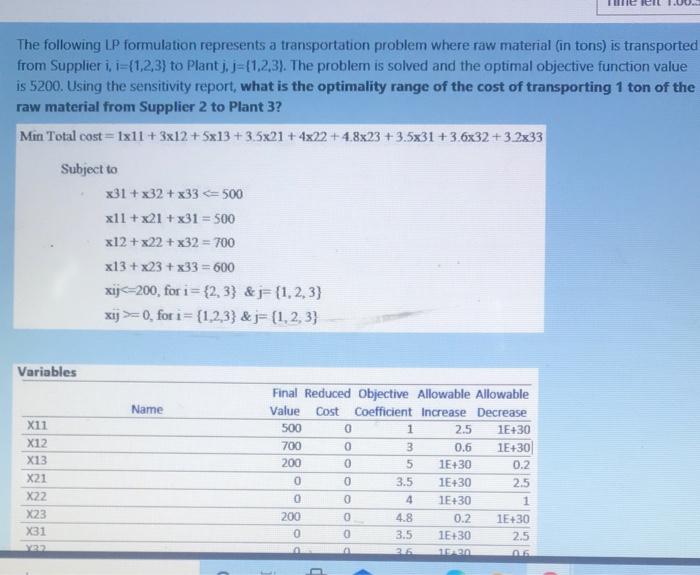
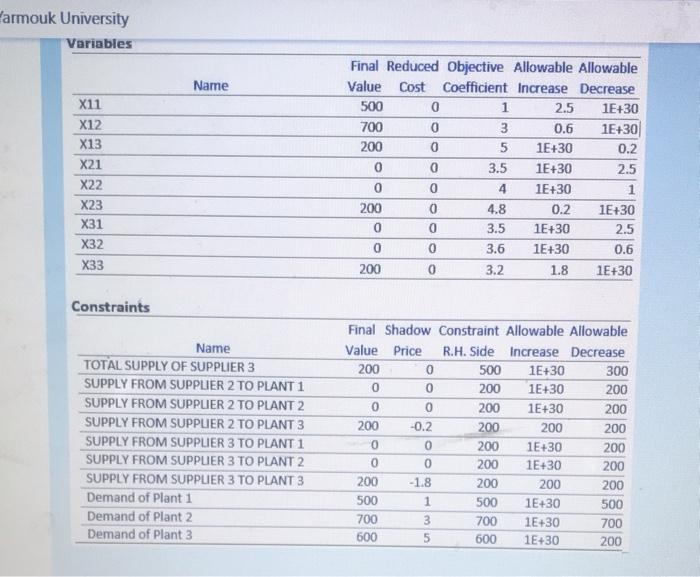
The following LP formulation represents a transportation problem where raw material (in tons) is transported from Supplier i. i={1,2,3} to Plant j.J={1,2,3). The problem is solved and the optimal objective function value is 5200. Using the sensitivity report, what is the optimality range of the cost of transporting 1 ton of the raw material from Supplier 2 to Plant 3? Min Total cost=1x11+ 3x12 + 5x13 +3.5x21 +4x22 +4,8x23 +3.5x31 +3.6x32+32x33 Subject to 31+ x32 + x33500 xll + x21 + x31 = 500 x12 + x22 + x32 = 700 x13 + x23 + x33 = 600 xij=0, for i= {1,2,3} &j= (1, 2, 3} Variables Name X11 X12 X13 X21 X22 X23 X31 Final Reduced Objective Allowable Allowable Value Cost Coefficient Increase Decrease 500 1 2.5 1E+30 700 3 0.6 1E+30 200 0 5 1E+30 0.2 0 0 3.5 1E+30 2.5 0 0 4 1E+30 1 200 4.8 0.2 1E+30 0 0 3.5 1E+30 2.5 . 25 1920 armouk University Variables Name X11 X12 X13 X21 X22 X23 X31 X32 X33 Final Reduced Objective Allowable Allowable Value Cost Coefficient Increase Decrease 500 0 1 2.5 1E+30 700 0 3 0.6 1E+30 200 0 5 1E+30 0.2 0 0 3.5 1E+30 2.5 0 0 4 1E+30 1 200 0 4.8 0.2 1E+30 0 0 3.5 1E+30 2.5 0 0 3.6 1E+30 0.6 200 0 1.8 1E+30 3.2 Constraints Name TOTAL SUPPLY OF SUPPLIER 3 SUPPLY FROM SUPPLIER 2 TO PLANT 1 SUPPLY FROM SUPPLIER 2 TO PLANT 2 SUPPLY FROM SUPPLER 2 TO PLANT 3 SUPPLY FROM SUPPLER 3 TO PLANT 1 SUPPLY FROM SUPPLER 3 TO PLANT 2 SUPPLY FROM SUPPLIER 3 TO PLANT 3 Demand of Plant 1 Demand of Plant 2 Demand of Plant 3 Final Shadow Constraint Allowable Allowable Value Price R.H. Side Increase Decrease 200 0 500 1E+30 300 0 0 200 1E+30 200 0 0 200 1E+30 200 200 -0.2 200 200 200 0 0 200 1E+30 0 200 1E+30 200 200 -1.8 200 200 200 500 1 500 1E+30 500 700 3 700 1E+30 700 600 5 600 1E+30 200 200 The following LP formulation represents a transportation problem where raw material (in tons) is transported from Supplier i. i={1,2,3} to Plant j.J={1,2,3). The problem is solved and the optimal objective function value is 5200. Using the sensitivity report, what is the optimality range of the cost of transporting 1 ton of the raw material from Supplier 2 to Plant 3? Min Total cost=1x11+ 3x12 + 5x13 +3.5x21 +4x22 +4,8x23 +3.5x31 +3.6x32+32x33 Subject to 31+ x32 + x33500 xll + x21 + x31 = 500 x12 + x22 + x32 = 700 x13 + x23 + x33 = 600 xij=0, for i= {1,2,3} &j= (1, 2, 3} Variables Name X11 X12 X13 X21 X22 X23 X31 Final Reduced Objective Allowable Allowable Value Cost Coefficient Increase Decrease 500 1 2.5 1E+30 700 3 0.6 1E+30 200 0 5 1E+30 0.2 0 0 3.5 1E+30 2.5 0 0 4 1E+30 1 200 4.8 0.2 1E+30 0 0 3.5 1E+30 2.5 . 25 1920 armouk University Variables Name X11 X12 X13 X21 X22 X23 X31 X32 X33 Final Reduced Objective Allowable Allowable Value Cost Coefficient Increase Decrease 500 0 1 2.5 1E+30 700 0 3 0.6 1E+30 200 0 5 1E+30 0.2 0 0 3.5 1E+30 2.5 0 0 4 1E+30 1 200 0 4.8 0.2 1E+30 0 0 3.5 1E+30 2.5 0 0 3.6 1E+30 0.6 200 0 1.8 1E+30 3.2 Constraints Name TOTAL SUPPLY OF SUPPLIER 3 SUPPLY FROM SUPPLIER 2 TO PLANT 1 SUPPLY FROM SUPPLIER 2 TO PLANT 2 SUPPLY FROM SUPPLER 2 TO PLANT 3 SUPPLY FROM SUPPLER 3 TO PLANT 1 SUPPLY FROM SUPPLER 3 TO PLANT 2 SUPPLY FROM SUPPLIER 3 TO PLANT 3 Demand of Plant 1 Demand of Plant 2 Demand of Plant 3 Final Shadow Constraint Allowable Allowable Value Price R.H. Side Increase Decrease 200 0 500 1E+30 300 0 0 200 1E+30 200 0 0 200 1E+30 200 200 -0.2 200 200 200 0 0 200 1E+30 0 200 1E+30 200 200 -1.8 200 200 200 500 1 500 1E+30 500 700 3 700 1E+30 700 600 5 600 1E+30 200 200