The following matching question involves induction and strong induction problems

1). Fill in column 1 with the letters from column 3 that match the description in column 2.

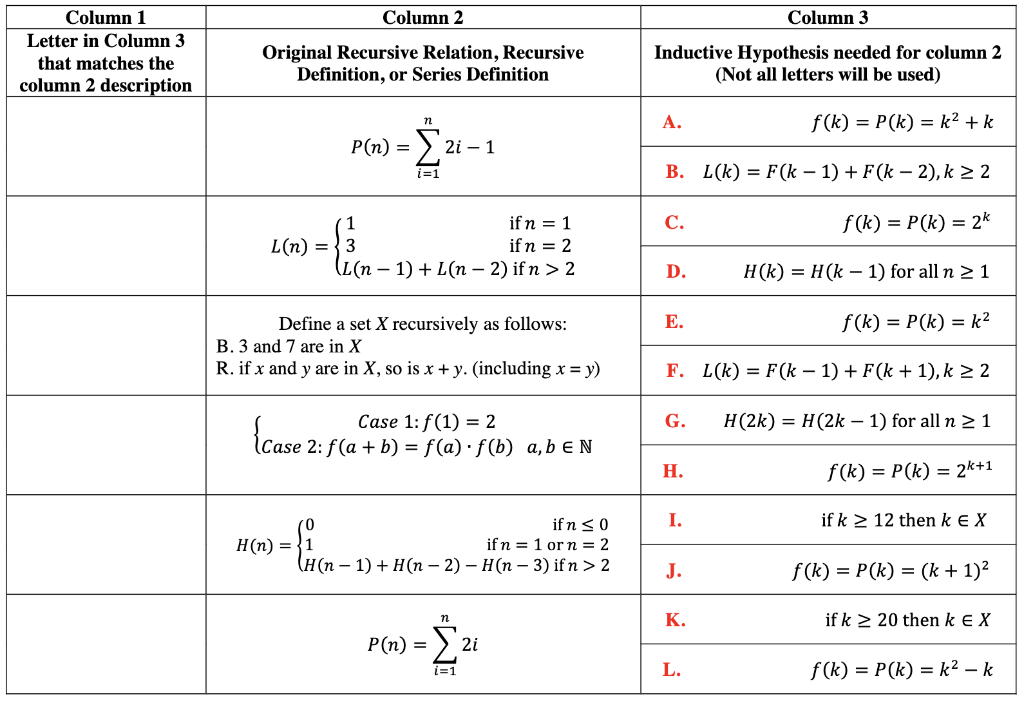
2). Which valid Inductive Hypotheses from column 1 above require Strong Induction to prove? List letters:

Column 2 Column 3 Column 1 Letter in Column 3 that matches the column 2 description Original Recursive Relation, Recursive Definition, or Series Definition Inductive Hypothesis needed for column 2 (Not all letters will be used) n A. f(k) = P(k) = ka + k P(n) = 2i - 1 i=1 B. L(k) = F(k 1) + F(k 2), k > 2 C. f(k) = P(k) = 24 if n = 1 L(n) = 3 if n = 2 (l(n 1) + L(n - 2) if n > 2 )(1+1 D. H(k) = H(k 1) for all n 2 1 E. f(k) = P(k) = k2 Define a set X recursively as follows: B. 3 and 7 are in X R. if x and y are in X, so is x + y. (including x = y) F. L(k) = F(k 1) + F(k + 1), k > 2 Case 1: 1= 2 G. H(2k) = H(2k 1) for all n > 1 {case 2:5(2 4969 = f(a) f) a,ben H. f(k) = P(k) = 2k+1 I. if k > 12 then k EX if n so H(n) = {1 if n = 1 or n = 2 (H(n-1) + H(n-2) - H(n-3) if n > 2 J. f(k) = P(K) = (k + 1)2 n K. if k > 20 then k EX P(n) = 2i i=1 L. f(k) = P(k) = k2 k Column 2 Column 3 Column 1 Letter in Column 3 that matches the column 2 description Original Recursive Relation, Recursive Definition, or Series Definition Inductive Hypothesis needed for column 2 (Not all letters will be used) n A. f(k) = P(k) = ka + k P(n) = 2i - 1 i=1 B. L(k) = F(k 1) + F(k 2), k > 2 C. f(k) = P(k) = 24 if n = 1 L(n) = 3 if n = 2 (l(n 1) + L(n - 2) if n > 2 )(1+1 D. H(k) = H(k 1) for all n 2 1 E. f(k) = P(k) = k2 Define a set X recursively as follows: B. 3 and 7 are in X R. if x and y are in X, so is x + y. (including x = y) F. L(k) = F(k 1) + F(k + 1), k > 2 Case 1: 1= 2 G. H(2k) = H(2k 1) for all n > 1 {case 2:5(2 4969 = f(a) f) a,ben H. f(k) = P(k) = 2k+1 I. if k > 12 then k EX if n so H(n) = {1 if n = 1 or n = 2 (H(n-1) + H(n-2) - H(n-3) if n > 2 J. f(k) = P(K) = (k + 1)2 n K. if k > 20 then k EX P(n) = 2i i=1 L. f(k) = P(k) = k2 k