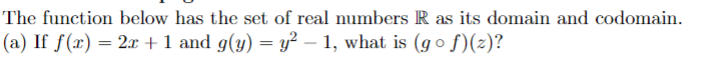
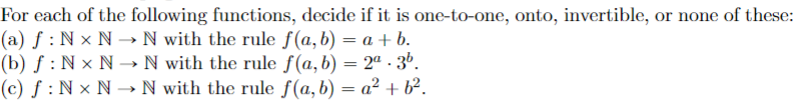
The function below has the set of real numbers R as its domain and codomain. (a) If f(x) = 2x + 1 and g(y) = y 1, what is (go f)(z)? Let c P({x, y, z}) P({x, y, z}) be the function with rule c(A) = {x, y, z} A, and let n: P({x, y, z}) {0, 1, 2, 3} be the function such that n(A) is the number of elements in the set A. Which composition is defined, con or noc? For the one that is defined, described the domain and the codomain, and give an arrow diagram for the function. Consider the relation R on the set A = {0, 1, 2, 3, 4, 5, 6} with the rule that R y if x - y is divisible by 3. Draw the one-set arrow diagram for R and Ro R, and describe the latter relation with an English sentence. For each of the following functions, decide if it is one-to-one, onto, invertible, or none of these: (a) f: N N N with the rule f(a, b) = a + b. (b) f: Nx N N with the rule f(a, b) = 2. 3b. (c) f: NxN N with the rule f(a, b) = a + b. Let S = {a,b,c}, and define a function c : P(S) P(S) by c(A) = S A. (a) Is the function c one-to-one? (b) Is the function conto? (c) Is the function c is invertible, then describe the inverse of c. If c is not invertible, explain why not. Let S = {a,b,c} and let c be the function of Exercise 5. Let n : P(S) {0, 1, 2, 3} be defined so that n(X) is the number of elements in X, and let s : {0, 1,2,3} P(S) be defined by Table 4-12. (a) Which composition is defined, c o s or soc? For the one that is defined, describe the domain and the codomain, and give an arrow diagram for the function. (b) Give an arrow diagram for son. Is son one-to-one? Is son onto? (c) Give an arrow diagram for no s. Is no s one-to-one? Is nos onto? i s(i) 0 is 1 {a} Table 4-12 2 {a.b} 3 {a,b,c} Let A be the set of letters in the English alphabet. For each of the following relations on A, decide if it is reflexive, irreflexive, transitive, or antisymmetric. (Each can satisfy more than one of these properties.) (a) R = {(a, ) A A: a immediately precedes in alphabetical order} (b) R = {(a, ) A A: a comes before 3 in alphabetical order} Let A = {1,2,3}. Give an example of a relation R on A that is (a) Transitive and reflexive but not antisymmetric. (b) Antisymmetric (c) Antisymmetric and reflexive but not transitive. and transitive but not reflexive. Let S = {1,2,3}. For each of the following relations on P(S), draw the arrow diagram and decide if the relation is reflexive, antisymmetric, or transitive. If it fails any of these prop- erties, give a specific example to illustrate this. If it has all three properties (i.e., if it is a partial ordering), give the corresponding Hasse diagram. (a) R = {(A, B) = P(S) P(S): A B} (b) R = {(A,B) P(S) P(S) : B A = {3}} (c) R3 = {(A, B) = P(S) P(S): AnB = } (d) R4 = {(A, B) P(S) P(S) : An B } (e) R5 = {(A,B) = P(S) P(S) : n(A) < n(B)}