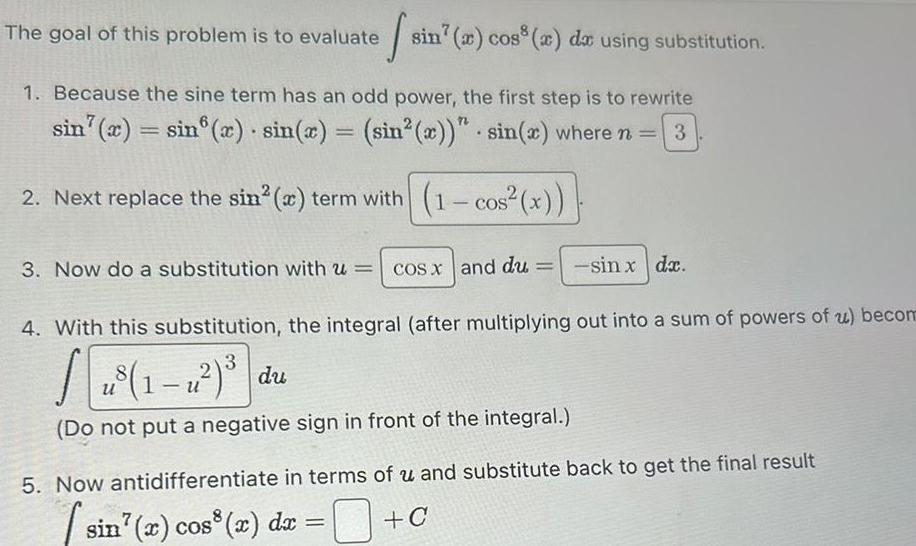
The goal of this problem is to evaluate sin sin(x) cos(x) da using substitution. 1. Because the sine term has an odd power, the first step is to rewrite sin(x)=sin(x) sin(x) = (sin(x))" sin(x) where n = 3 . . 2. Next replace the sin (x) term with (1-cos (x)) 3. Now do a substitution with u = = COS X and du = -sin x dx. 4. With this substitution, the integral (after multiplying out into a sum of powers of u) becom - (Do not put a negative sign in front of the integral.) 5. Now antidifferentiate in terms of u and substitute back to get the final result sin(x) cos(x) dx = +C