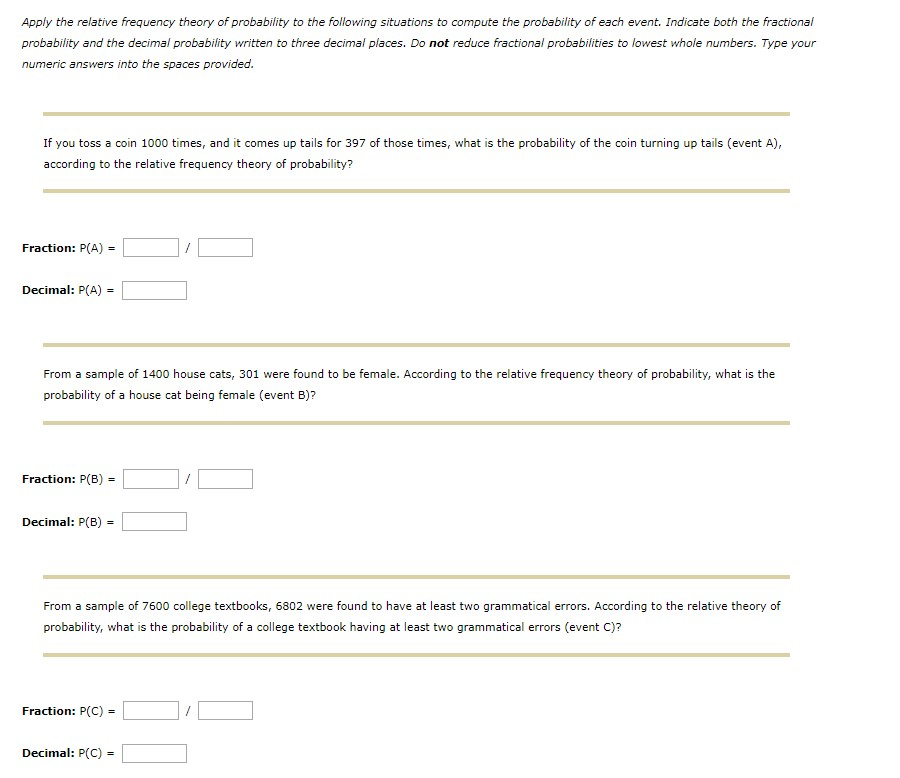
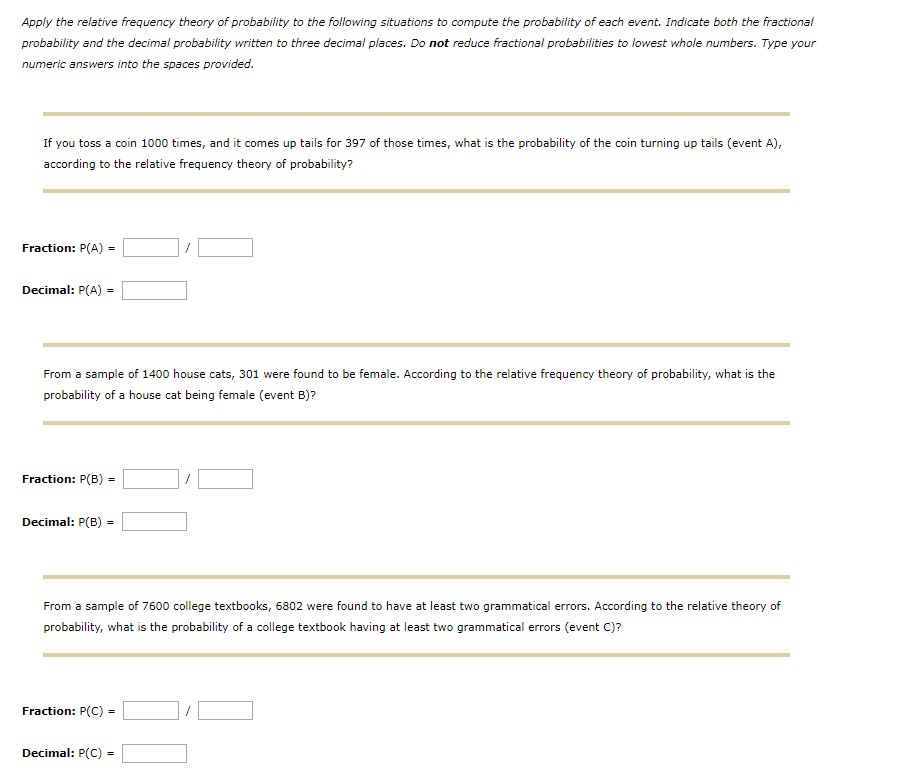
The going with table tends to school understudies at a local school. One understudy is picked capriciously. Offer your reaction as a decimal out to at any rate 4 spots.

Green bean Sophomore Junior Senior Total

Live On Campus 2294 2188 1724 1888 8094

Live Off Campus 3831 4286 4925 822 13864

Absolute 6125 6474 6649 2710 21958

a) Find the probability that the understudy lives off grounds or is a lesser.

b) Find the probability that the understudy lives close by and is a senior.

c) Find the probability that the understudy is a green bean given that they live close by.

d) Are the events Freshman and Live on Campus generally random? Why?

Surely, since the P(Freshman | Live On Campus) = P(Freshman)

Surely, since P(Freshman ?? Live On Campus) = 0.1045 ? 0

No, since P(Freshman ?? Live On Campus) = 0.1045 ? 0

Surely, since you can be a green bean that lives close by

No, since P(Freshman ?? Live On Campus) = 0.1045 ? P(Freshman)*P(Live On Campus) = 0.1028

To be sure, since P(Freshman ?? Live On Campus) = 0.1045 ? P(Freshman)*P(Live On Campus) = 0.1028

e) Are the events Freshman and Live on Campus self-sufficient? Why?

To be sure, since the P(Freshman | Live On Campus) = P(Freshman)

To be sure, since P(Freshman ?? Live On Campus) = 0.1045 ? 0

No, since P(Freshman ?? Live On Campus) = 0.1045 ? 0

To be sure, since you can be a green bean that lives close by

No, since P(Freshman ?? Live On Campus) = 0.1045 ? P(Freshman)*P(Live On Campus) = 0.1028

To be sure, since P(Freshman ?? Live On Campus) = 0.1045 ? P(Freshman)*P(Live On Campus) = 0.1028

The chiefs at a close by association asked with respect to whether they were excited about getting position planning. Responses are summarized by work type (salaried or hourly), and whether the agent is captivated (yes or no) in work planning.

Salaried Hourly Total

undoubtedly 68 56 124

no 11 44 55

hard and fast 79 100 179

Figure the probability that a laborer is salaried. Offer your reaction as a decimal, definite to in any occasion three decimal spots.

p salaried =

At that point, figure the probability that a specialist who is enthusiastic about getting ready is salaried. Offers your reaction as a decimal, definite to at any rate three decimal spots.

p salaried/yes=

Finally, use the results from the two preceeding assessments to choose if business tpe and interest in getting ready are self-sufficient.

No, the two events are not self-governing.

For sure, the two events are free.

i10i

The latest overview of subjectively picked Pennsylvanians exhibits that the probability of someone

coming from a country establishment is .65, the probability of coming from a metropolitan establishment is

.20, and the probability of coming from an establishment portrayed as nor is .15

From an unpredictable decision of 20 Pennsylvanians, and expecting the data fit a binomial course:

a) Find the probability that at any rate 10 come from a metropolitan establishment.

b) Find the probability that five come from a natural establishment.

c) Find the probability that at most two say that their region is neither common nor metropolitan.

d) Find the probability that ?(7

e) What tone was the canine

1)Bob Neverready has a flexible TV. The TV uses two batteries and both of them are dead.

Ricochet opens another pack of four incredible batteries and dumps them on the table.

By then he opens the TV and dumps the two dead batteries on the table with the incredible ones.

The batteries get worked up and Bob no longer acknowledges which can't avoid being which. (Has this reliably happened to you?)

In the occasion that Bob removes two batteries from the table aimlessly and spots them into the TV, what is the probability that he picked two extraordinary batteries and that the TV will work?

The typical joblessness rate in California in August 2020 was 11.4%.

2)Assume that 550 employable people in California were picked indiscriminately in August 2020.

What is the by and large expected worth of the amount of people in the model who were jobless?

Round your reaction to one decimal point

3)A deck of 52 playing a game contains four suits, each with thirteen cards.

In a particular game, a hand contains eleven cards picked subjectively without replacement.

What is the probability that a hand will have decisively 7 cards in a comparative suit?

Round your reaction to three decimal spots.

In the event that it's not all that much difficulty, help! Thankful to you

Apply the relative frequency theory of probability to the following situations to compute the probability of each event. Indicate both the fractional probability and the decimal probability written to three decimal places. Do not reduce fractional probabilities to lowest whole numbers. Type your numeric answers into the spaces provided. If you toss a coin 1000 times, and it comes up tails for 397 of those times, what is the probability of the coin turning up tails (event A), according to the relative frequency theory of probability? Fraction: P(A) = Decimal: P(A) = From a sample of 1400 house cats, 301 were found to be female. According to the relative frequency theory of probability, what is the probability of a house cat being female (event B)? Fraction: P(B) = Decimal: P(B) = From a sample of 7600 college textbooks, 6802 were found to have at least two grammatical errors. According to the relative theory of probability, what is the probability of a college textbook having at least two grammatical errors (event C)? Fraction: P(C) = Decimal: P(C) =14. 1IIIv'hich one of the following statements is FALSE? multiple choice question 1. The probability of an everrt occurring is always between 1 and +1. 2. The probability that an event will occur given that some other event has already happened is known as conditional probability. 3. Prior probabilities. are estimates before the market survey. 4. The joint probability of two events E1 and E2 is expressed as P{E1 and E2}. 5. Bayes' Theorem is an extension of conditional probability theory used to revise calculated probabilities when new information is known. 42. The probability of event A happening is 3/5 and the probability of event B happening is 2/3. What is the probability of only event A happening, i.e. event A happening and event B not happening?* (2 Points) 3/5 1/5 O 4/5 2/5 43. How many different ways can 5 boys and 5 girls form a circle with boys and girls alternate?* (2 Points) 28800 14400 2880 L