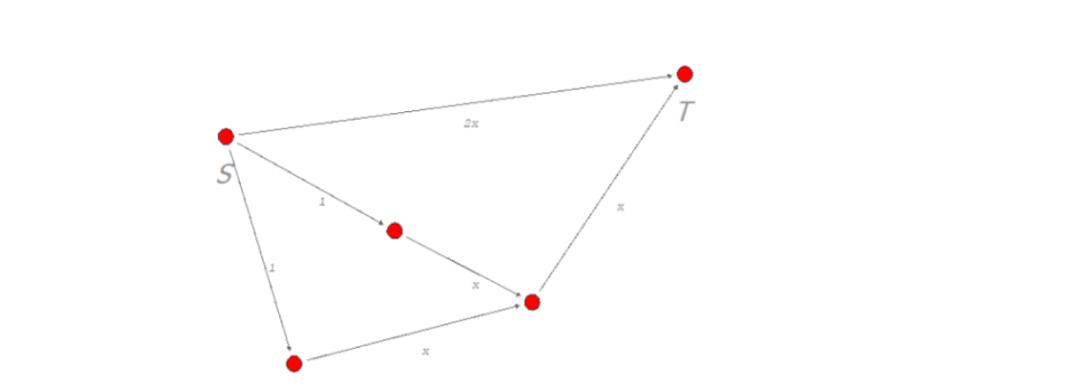
The graph below indicates an instance of a routing game. The source is labeled as S and the sink is labeled as T. There is a mass 1 of flow that must be routed from source to sink. The latency functions for each edge are labeled next to that edge. A latency function of 1 means that the latency of this edge is always 1, regardless of load. A latency function of a means that the latency of this edge is equal to the load xe on this edge. A latency function of 2x means that the latency of this edge is equal to twice the load xe on this edge. Recall that the load is the total amount of flow that passes over a given edge. Formally, this is the sum of the flow assigned to paths that use the edge e: Xe = {P: e is on Pi} fp. S (c) (d) Label the paths from source to sink in this graph. How many source-sink paths are there? Consider the flow that routes all agents on the edge with latency 2x directly between source and sink. What is the latency of this path at this flow? Is this flow an equilibrium? Briefly explain. Find an equilibrium flow for this game. Verify that it is an equilibrium. Let's add some taxes into this problem. Suppose that we were to impose a tax of 0 on all edges with latency function of 1, a tax of x on edges that have a latency function of x, and a tax of 2x on the edge that has a latency function of 2x. Suppose that agents evaluate total cost as: Ce(re)=le (te) + Te(xe) where le(re) is the latency of edge e (given the load xe) and Te(re) is the tax on edge e (given the load on te). So, for example, the total cost of an edge with latency function x would now be 2x, and the total cost of an edge with latency function 1 would still be 1 (it has a tax of 0). Suppose that agents seek to minimize the total cost of the path that they choose. Find the equilibrium flow with these new cost functions. Show that this flow has a lower average la- tency than the equilibrium flow that you found in part (c). You may find the formula for average latency of a flow f useful here: l(f) = 1(P, f) fp +1(P2, f) fp +1(P3, f). fP3 where (Pi, f) denotes the latency of path P given the flow f, and fp, denotes the amount of flow assigned to path Pi. Here, I'm just asking about average latency, so you'll want to take the flow that you find in this part and plug it back into the original game (without taxes).