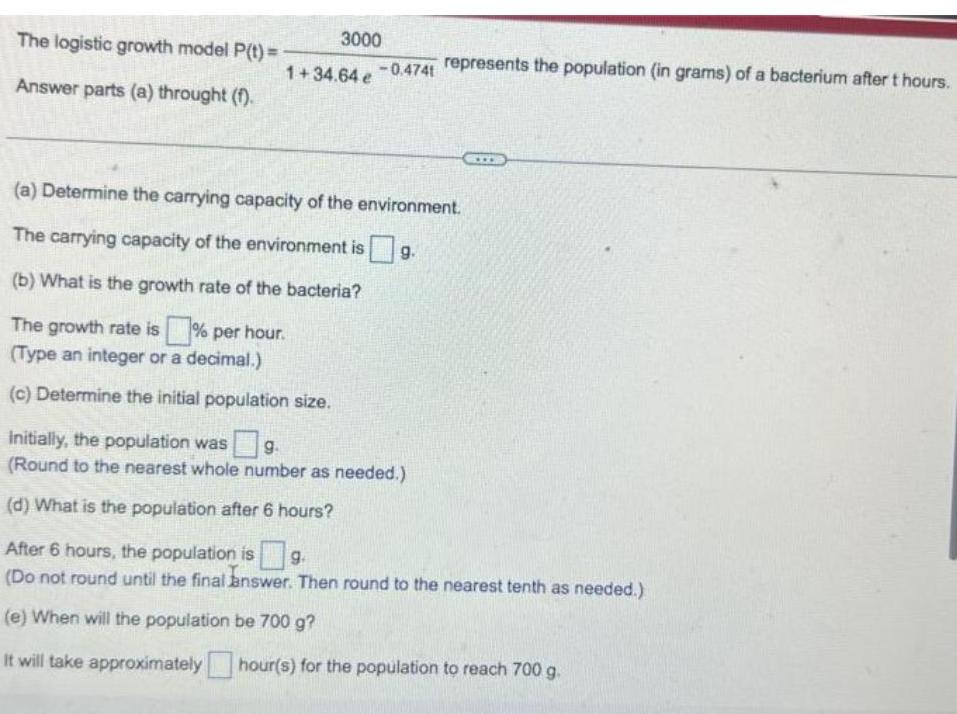
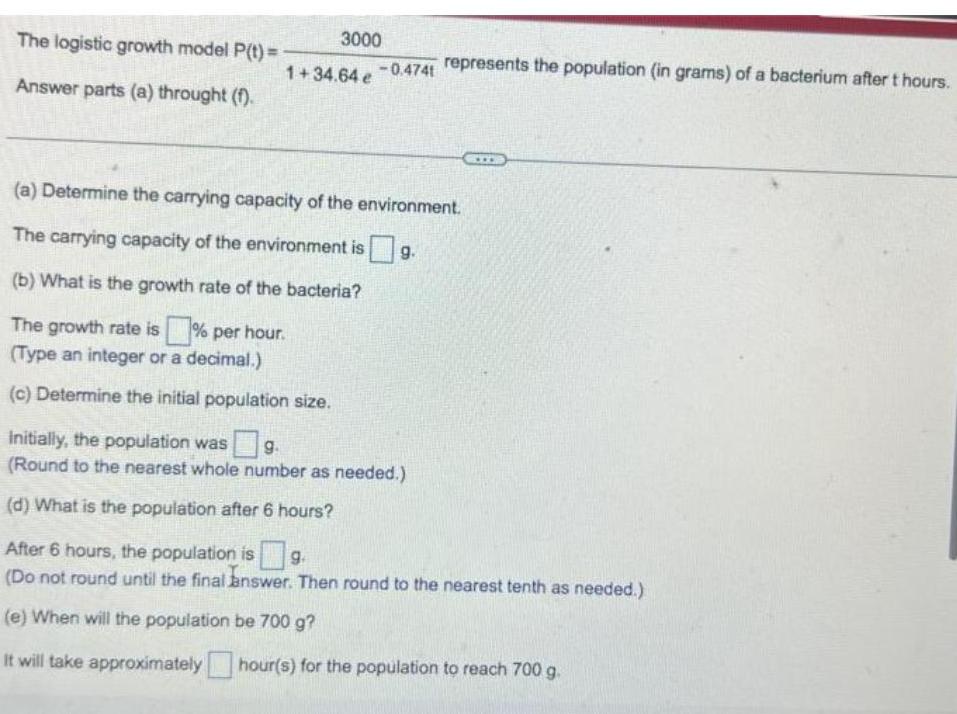
The logistic growth model P(t)= 3000/1+34.64 e -0.4741 represents the population (in grams) of a bacterium after t hours.Answer parts (a) throught (f).(a) Determine the carrying capacity of the environment.The carrying capacity of the environment is g.(b) What is the growth rate of the bacteria?The growth rate is% per hour.(Type an integer or a decimal.)(c) Determine the initial population size.Initially, the population was g.(Round to the nearest whole number as needed.)(d) What is the population after 6 hours?After 6 hours, the population is g.(Do not round until the final answer. Then round to the nearest tenth as needed.)(e) When will the population be 700 g?It will take approximatelyhour(s) for the population to reach 700 g.