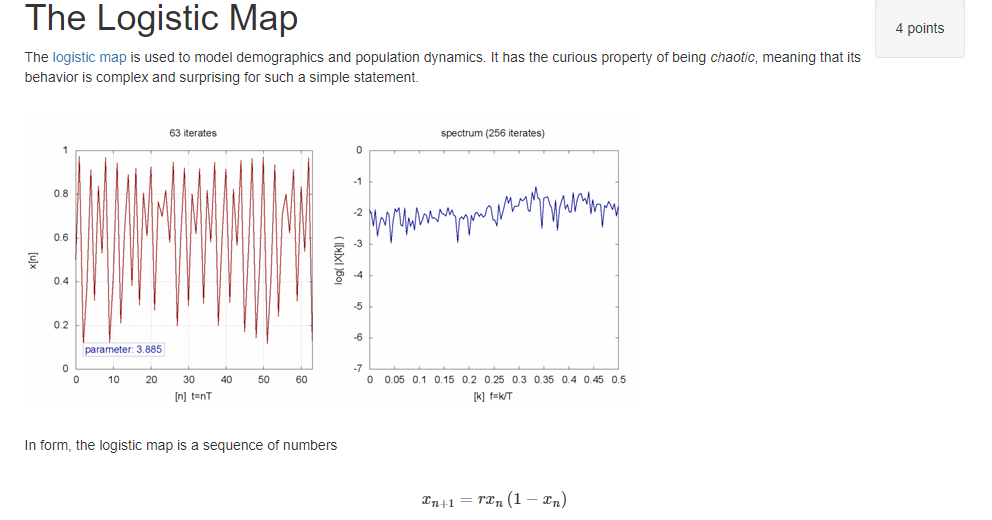
The Logistic Map 4 points The logistic map is used to model demographics and population dynamics. It has the curious property of being chaotic, meaning that its behavior is complex and surprising for such a simple statement. 63 iterates spectrum (256 iterates) 0 0.8 "rs/tri, 0.6 log IX[k]) 0.4 -5 0.2 -6 parameter: 3.885 0 0 10 20 40 50 60 30 in) tent -7 0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 [k] fak/T In form, the logistic map is a sequence of numbers 2n+1 = ran(1 - 2n) In form, the logistic map is a sequence of numbers Xn+1 = ran (1 - In) where r is a parameter and I, is the previous value in the sequence, 2 [0,1]. For instance, if we take 20 = 0.5 for r = 2.25, we obtain the following sequence: 0.5 0.5537109375 0.55600905418396 0.555441718161191 0.5555839857465039 0.555548446189198 0.5555573327834229 0.5555551112414819 0.5555556666336298 0.5555555277860093 0.5555555555555555... which clearly approaches Implement a function x_ (note the underscore) which accepts arguments r and x and returns the logistic map 2n+1 as defined above. For instance, the following should hold true of your function: x_(2.25, 0.5) == 0.5625 x_(3,0.8) == 0.48 The Logistic Map 4 points The logistic map is used to model demographics and population dynamics. It has the curious property of being chaotic, meaning that its behavior is complex and surprising for such a simple statement. 63 iterates spectrum (256 iterates) 0 0.8 "rs/tri, 0.6 log IX[k]) 0.4 -5 0.2 -6 parameter: 3.885 0 0 10 20 40 50 60 30 in) tent -7 0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 [k] fak/T In form, the logistic map is a sequence of numbers 2n+1 = ran(1 - 2n) In form, the logistic map is a sequence of numbers Xn+1 = ran (1 - In) where r is a parameter and I, is the previous value in the sequence, 2 [0,1]. For instance, if we take 20 = 0.5 for r = 2.25, we obtain the following sequence: 0.5 0.5537109375 0.55600905418396 0.555441718161191 0.5555839857465039 0.555548446189198 0.5555573327834229 0.5555551112414819 0.5555556666336298 0.5555555277860093 0.5555555555555555... which clearly approaches Implement a function x_ (note the underscore) which accepts arguments r and x and returns the logistic map 2n+1 as defined above. For instance, the following should hold true of your function: x_(2.25, 0.5) == 0.5625 x_(3,0.8) == 0.48