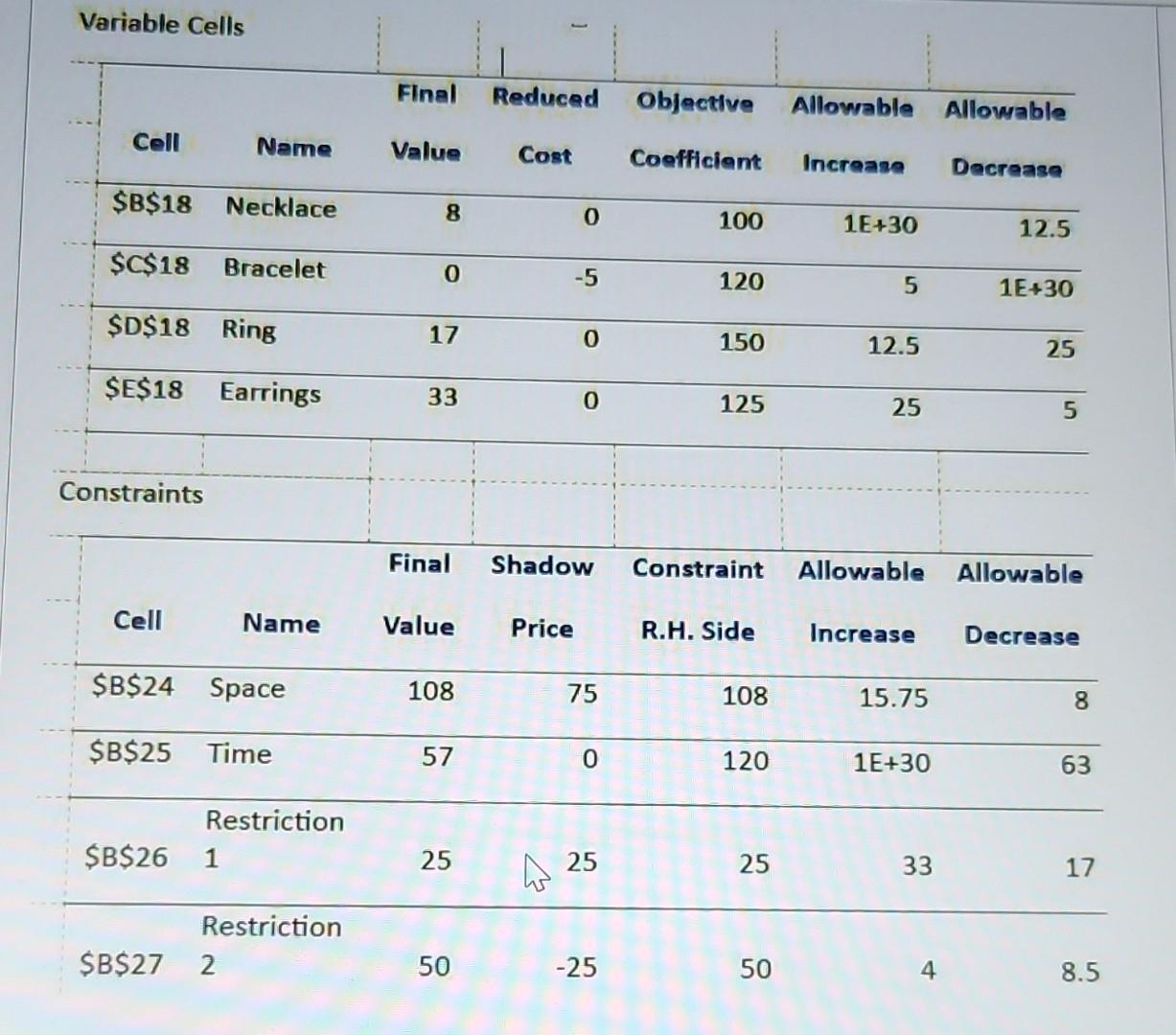
The LP problem whose output follows determines how many necklaces, bracelets, rings, and earrings a jewelry store should stock. The objective function measures profit; it is assumed that every piece stocked will be sold. Constraints measure display space in units, time to set up the display in minutes and two marketing restrictions. \begin{aligned} & \\ & \\ & 11 \\ & \( >2\end{aligned} \) Use the output to solve and answer the following question. By how much will marketing restriction 1 be exceeded? \begin{tabular}{|c|c|c|c|c|c|c|} \hline \multicolumn{7}{|c|}{ Variable Cells } \\ \hline & & Final & Reduced & Objective & Allowable & Allowable \\ \hline Cell & Name & Value & Cost & Coefficient & Increasa & Decrease \\ \hline \$B\$18 & Necklace & 8 & 0 & 100 & 1E+30 & 12.5 \\ \hline$C$18 & Bracelet & 0 & -5 & 120 & 5 & 1F+30 \\ \hline \$D\$18 & Ring & 17 & 0 & 150 & & \\ \hline & & & & & 12.5 & 25 \\ \hline \$E\$18 & Earrings & 33 & 0 & 125 & 25 & 5 \\ \hline \multicolumn{7}{|l|}{ Constraints } \\ \hline & & Final & Shadow & Constraint & Allowable & Allowable \\ \hline Cell & Name & Value & Price & R.H. Side & Increase & Decrease \\ \hline$B$24 & Space & 108 & 75 & 108 & 15.75 & 8 \\ \hline$B$25 & Time & 57 & 0 & 120 & 1E+30 & 63 \\ \hline & Restriction & & & & & \\ \hline$B$26 & 1 & 25 & b25 & 25 & 33 & 17 \\ \hline$B$27 & \begin{tabular}{l} Restriction \\ 2 \end{tabular} & 50 & -25 & 50 & 4 & 8.5 \\ \hline \end{tabular} 4 1 0 3