The Mayflower Manufacturing Company produces a product on a number of machines. When a machine breaks down, it must be repaired; and it takes either one, two or three days for the repair to be completed. Every time a machine breaks down, the cost to the company is an estimated R2 000 per day in lost production until the machine is repaired.

The company would like to know if it should implement a machine maintenance program at a cost of R20 000 per year that would reduce the frequency of breakdowns and thus the time for repair. The maintenance program would result in the following continuous probability function for time between breakdowns:

f (x) = x/18; 0 < x<6 weeks; where x = weeks between machine breakdowns

The reduced repair time resulting from the maintenance program is defined by the following discrete probability distribution:

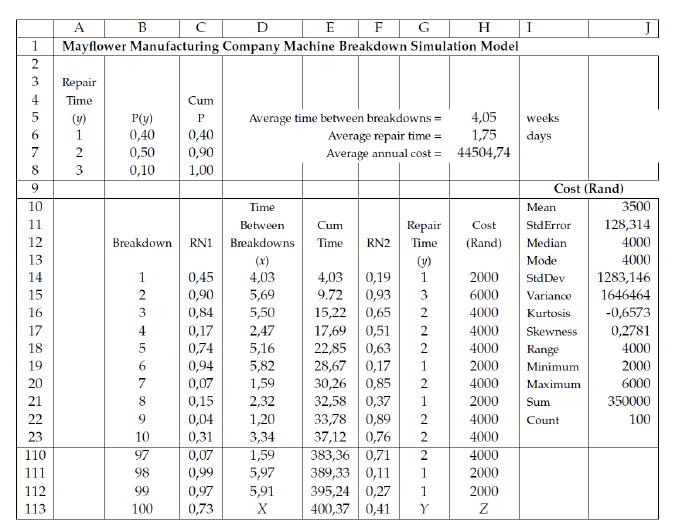
Machine Repair Time (y days)	Probability of Repair Time (P(y))
1	0.40
2	0.50
3	0.10

Table 2, below represents a spread sheet simulation model of the breakdown and repair processes in the maintenance program and the resulting costs. The spread sheet is frozen at row 24 to show the first 10 breakdowns and the last 4.

(a) Derive an equation for generating x given the random number r. (3 marks)

(b) Write down the formula for determining X in the spread sheet cell D113. (1mark)

(c) What is the average time between breakdowns over the last four breakdowns in the simulation run? (2 marks)

(d) What is the expected machine repair time resulting from the maintenance program? (2 marks)

(e) What is the repair time of the 100th breakdown in the simulation run? (1 mark)

(f) What is the repair cost of the 100th breakdown in the simulation run? (2 mark)

(g) What is the input range for creating the descriptive statistics in the spread sheet? (1 mark)

(h) Use the descriptive statistics to draw conclusions about the characteristics of the probability distribution of the output variable of the simulation. (3 marks)

(i) Calculate the lower limit of a 95% confidence interval for the cost. (5 marks)
 

E F G I A D H. 1 Mayflower Manufacturing Company Machine Breakdown Simulation Model 3. Repair 4 Time Cum P(y) 0,40 0,50 Average time between breakdowns = Average repair time = 4,05 1,75 Average annual cost = 44504,74 weeks (y) 1 P 0,40 0,90 6. days 7 2 3 0,10 1,000 9. Cost (Rand) 10 Time Mean 3500 11 Between Cum Repair Cost StdError 128,314 12 Breakdown RN1 Breakdowns Time RN2 Time (Rand) Median 4000 13 (x) 4000 (v) 1. Mode 14 1 0,45 4,03 5,69 5,50 2,47 5,16 5,82 1,59 2,32 4,03 9.72 0,19 0,93 2000 StdDev 1283,146 15 0,90 3 6000 Variance 1646464 0,84 0,17 15,22 0,65 4000 -0,6573 0,2781 16 2 Kurtosis 17 0,51 22,85 0,63 28,67 0,17 30,26 0,85 0,37 33,78 0,89 37,12 0,76 383,36 0,71 389,33 0,11 395,24 0,27 400,37 0,41 4 17,69 2 4000 Skewness 18 5 0,74 0,94 0,07 0,15 0,04 0,31 4000 4000 Range Minimum 19 1 2000 2000 20 7 4000 Maximum 6000 21 8. 32,58 1 2000 Sum 350000 22 9. 1,20 4000 Count 100 23 10 3,34 4000 110 97 0,07 0,99 0,97 0,73 1,59 4000 111 98 5,97 1 2000 112 99 5,91 1 2000 113 100 X Y