The objective of this HW is to use the ode45 command in Matlab to solve the state-space problems we have previously set up. Taken from Matlab Help, the syntax for ode45 is: [T,Y] = ode45(odefun,tspan,y0) Where the input arguments are: Y = the vector containing the (solved) equations describing the state variables T = time column vector defining the integration interval tspan = the time vector over which your equations will be solved y0 = your initial conditions and odefun = a function file that you must define in a separate m-file and that contains the RHS of your state-space equations in matrix form.

%%

The following contains the code for solving the simple example of a mass attached to a spring, and plotting the state variables x and v.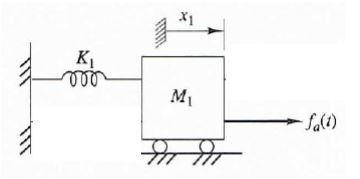

% this file is saved as simple.m

% This example code demonstrates how to use the function 'ode45' to solve % equations of motion when they are put into state-space form

% the state-variable matrix exists in the function file 'simple_fn' % The equations are derived from a simple translation system % where a single mass is attached to a spring and there is a single input time=linspace(1,50,1000); %this creates 1000 steps between 1 and 50 % time=[1:50]; %this creates 50 steps between 1 and 50. Note the impact % of using fewer steps %set initial conditions and system constants init_cond=[0 0]; k=1; m=1;

%% % Solve ODE. notice how the additional constant parameters k and m % are passed in using the "@(t,x)" operator, which tells ode45 that the % first two parameters passed into "simple_fn" are time and the state [t,xdot]=ode45(@(t,x) simple_fn(t,x,k,m),time,init_cond); %plot the state variables as a function of time plot(t,xdot); title(['Example: Simple mass-spring system. f_a(t) = sin(t)']) legend('x', 'v') xlabel('time') ylabel('State Variables')

%%

% this file is saved as simple_fn.m % this function file contains the state-variable equations for a system % containing 1 mass and 1 spring, with applied force fa(t) function [xdot]=simple_fn(t,x,k,m) xdot = [0, 1;... -k/m, 0]*x+... [0; 1]*sin(t); % a simple external forcing fn end

PROBLEM STATEMENT:

Run the code as provided to get plots of the state variables x and v in response to a simple external forcing function sin(t).

EDIT:

Since this is a system dynamics problem using matlab, here is the Equation of Motion of a mass on frictionless wheels with force f_a(t) applied to mass M_1, resisted by spring with constant K_1, displacement from initial position x(t), and time t.

EoM of system: f_a(t) = M_1 * x_1''(t) + K_1 * x(t) Also, I believe v and xdot are basically the same. Can someone clarify the difference between t and time? Also, what do I put for input x? But most importantly, how do I right the function line in the beginning? What are my main inputs and outputs for the whole code (I think for the simple.m file)?