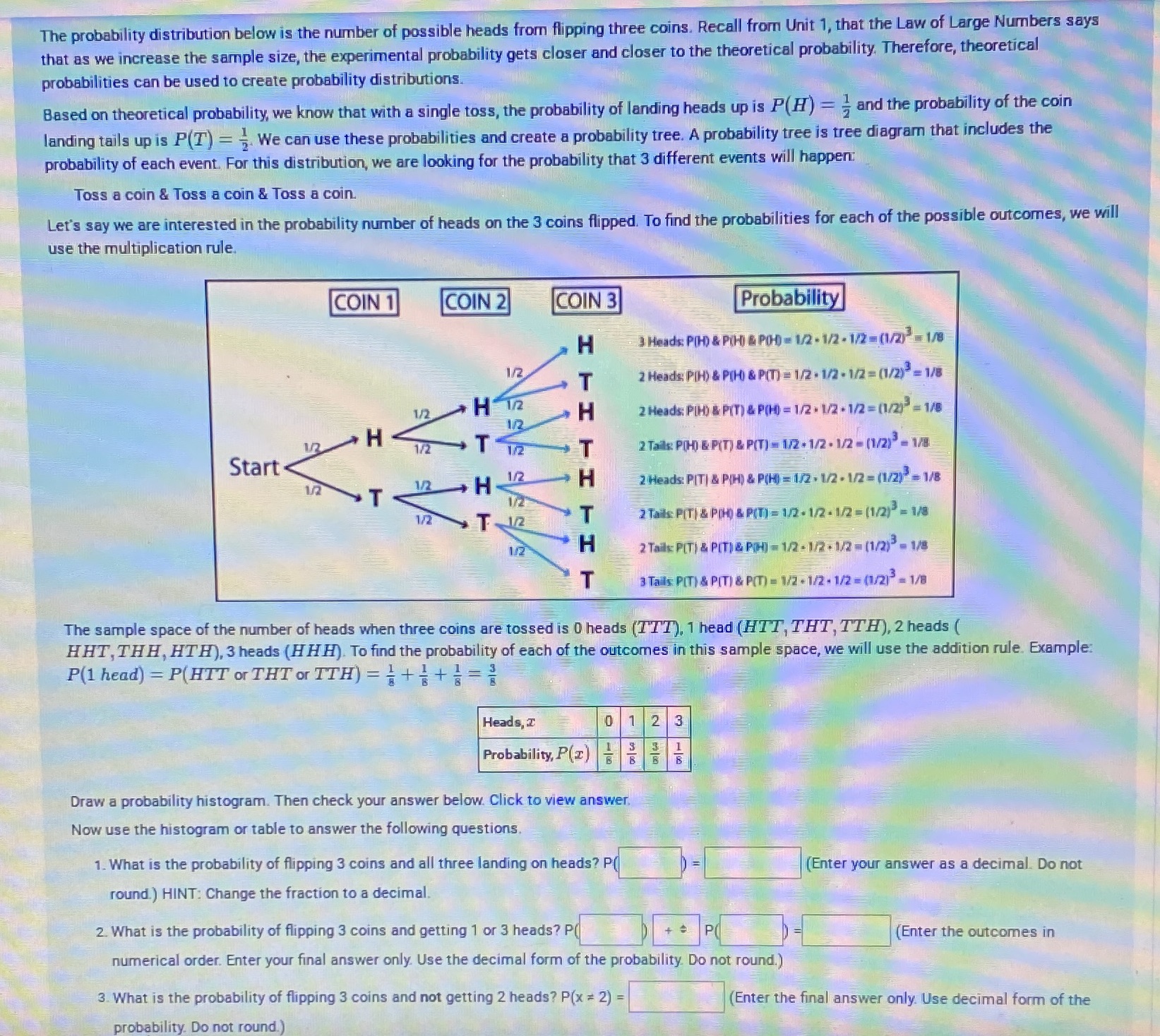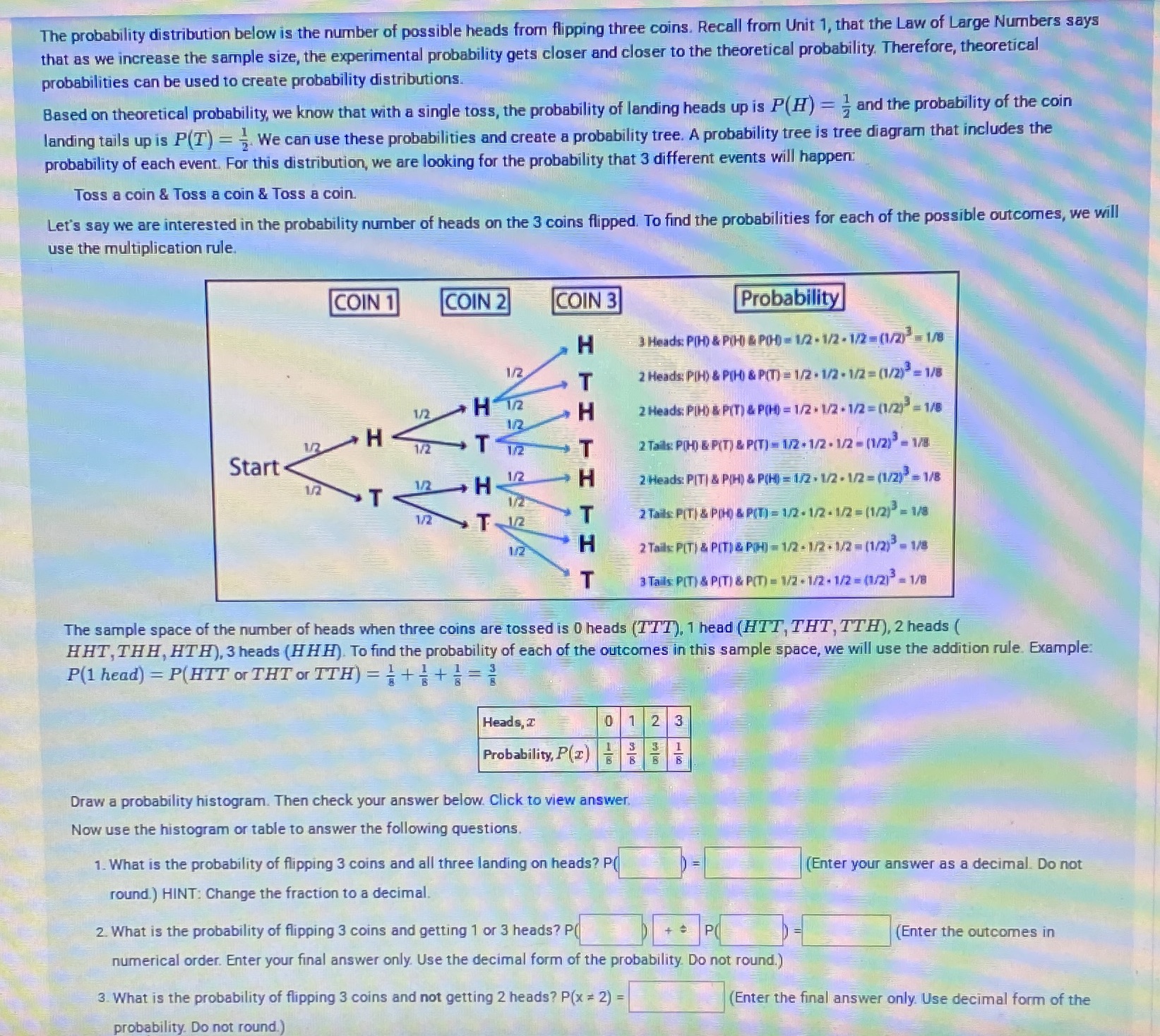
The probability distribution below is the number of possible heads from flipping three coins. Recall from Unit 1, that the Law of Large Numbers says that as we increase the sample size, the experimental probability gets closer and closer to the theoretical probability. Therefore, theoretical probabilities can be used to create probability distributions. Based on theoretical probability, we know that with a single toss, the probability of landing heads up is P(H ) = - and the probability of the coin landing tails up is P(T) = . We can use these probabilities and create a probability tree. A probability tree is tree diagram that includes the probability of each event. For this distribution, we are looking for the probability that 3 different events will happen Toss a coin & Toss a coin & Toss a coin. Let's say we are interested in the probability number of heads on the 3 coins flipped. To find the probabilities for each of the possible outcomes, we will use the multiplication rule. COIN 1 COIN 2 COIN 3 Probability H Heads P() & PUH- & PO-D = 1/2 - 1/2 - 1/2 -(1/2) =1/8 1/2 T 2 Heads PTH) & P(H) & P() = 1/2 . 1/2 - 1/2 = (1/2) =1/8 1/2 H 12 H 2 Heads PITA PIT) & P(H) = 1/2 . 1/2 - 1/2 = (1/2) = 1/8 H 1/2 T 2 Tails POP- & P(T) & P(T) - 1/2 - 1/2 . 1/2 - (1/2) - 1/8 Start 1/2 . H 2 Heads: PIT] & P(H) & PUH - 1/2 . 1/2 - 1/2 =(1/2) =1/8 1/2 1/2 T 2 Tails PITI & POD & PITI = 1/2 - 1/2 - 1/2 = (1/2) = 1/8 H 2 Tails PIT) & PITI &PH) - 12- 12.1/2-(1/2) - 1/8 3 Ta Is PIT) & PIT) & PIT) = 1/2 - 1/2 - 1/2 = (1/215 = 1/8 The sample space of the number of heads when three coins are tossed is 0 heads (TTT), 1 head (HTT, THT, TTH), 2 heads ( HHT, THH, HTH), 3 heads (HHH). To find the probability of each of the outcomes in this sample space, we will use the addition rule. Example: P(1 head) = P(HTT or THT or TTH) = = + + = Heads, I 0 1 2 3 Probability, P(z) 5 5 6 5 Draw a probability histogram. Then check your answer below. Click to view answer. Now use the histogram or table to answer the following questions. 1. What is the probability of flipping 3 coins and all three landing on heads? P( (Enter your answer as a decimal. Do not round.) HINT: Change the fraction to a decimal. 2. What is the probability of flipping 3 coins and getting 1 or 3 heads? P( ( Enter the outcomes in numerical order. Enter your final answer only. Use the decimal form of the probability Do not round.) 3. What is the probability of flipping 3 coins and not getting 2 heads? P(x = 2) = Enter the final answer only. Use decimal form of the probability. Do not round.)