Question
the question:- Consider the polynomial p(x)=5x^39x^227x5. a) The equation p(x)=0 has a rational root. Find this by applying theorem 7 in the course literature. b)

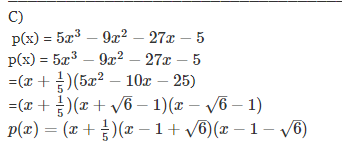
the question:-
Consider the polynomial p(x)=5x^39x^227x5.
a) The equation p(x)=0 has a rational root. Find this by applying theorem 7 in the course literature.
b) Use polynomial division and square completion to find the other roots of p(x). For polynomial division, you do not need to show all the steps, it is enough to enter the quotient and remainder.
c) Factorize p(x), that is, write p(x) as a product of polynomials of degree 1.Your solution must be well written and your conclusion clearly formulated. Explain reasoning using both text and mathematical symbols. Only calculations are not accepted.All theorems in the course literature may be used without proof.
my answer:-
Since x=...... is a root, (x+ 15) is a factor of p(x).If we divide p(x) by (x+ 15) we get-----We will factor......It will be impossible to split the midterm here,so we use the formula x = ....
Other roots of p

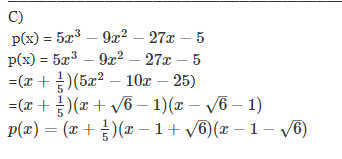
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


