the question is given in the picture below

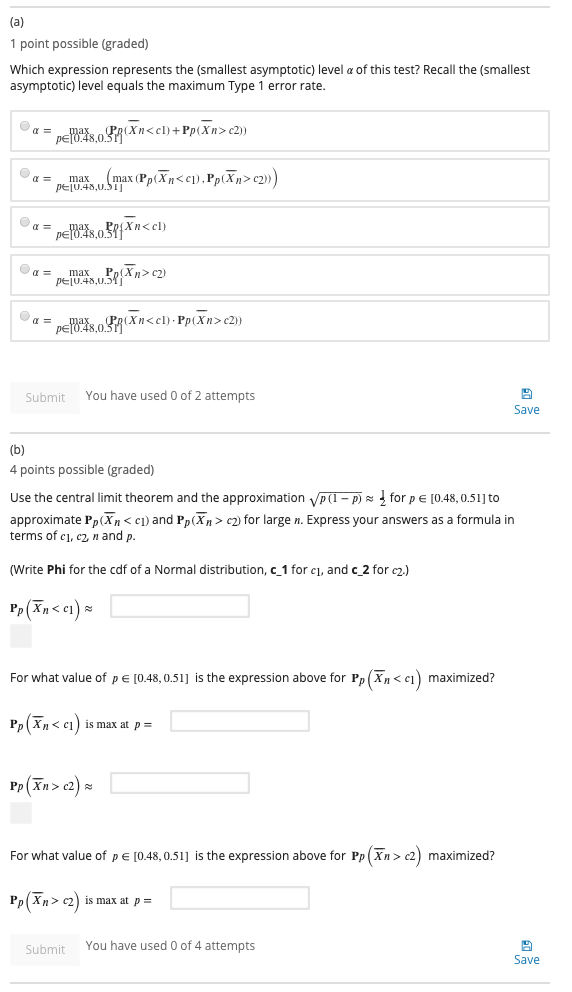
1A Union-Intersection Test N Bookma rk this page Let M, , X\" be i.i.d. Bernoulli random variables with unknown parameter p E (o, 1}. Suppose we want to test H1] : p e [0.43, 0.51] vs H111! e [1143, I151] We want to construct an asymptotic test W for these hypotheses using in. For this problem, we specically consider the family of tesm wclgwhere we reject the null hypothesis if either fr: 1:13 1143 or Y" > :2 2 I151 for some :1 and czthat may depend on n, i.e. Waltz: 1 ((3% :1) u (E. 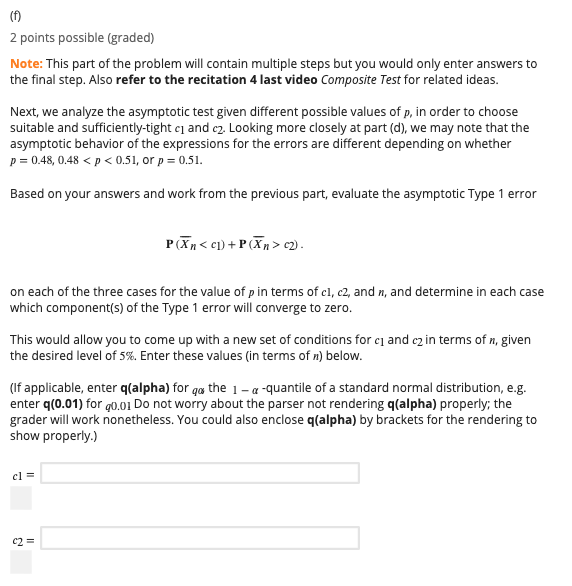> 1:23) where c] c2)) 1 = max PE10.48,0.51] (max (Pp(Xnc2)>) On= max On= DE:48.0. PQ(Xnc2)) Submit You have used 0 of 2 attempts Save (b) 4 points possible (graded) Use the central limit theorem and the approximation vp (1 - p) = _ for pe [0.48, 0.51] to approximate Pp(X, c2) for large n. Express your answers as a formula in terms of cl, cz n and p. (Write Phi for the cdf of a Normal distribution, c_1 for cj, and c_2 for cz.) Pp (Xn (2) = For what value of pe [0.48, 0.51] is the expression above for Pp (Xn > c2) maximized? Pp(Xn> c2) is max at p = Submit You have used 0 of 4 attempts Save(c) 1 point possible (graded) Next, we combine the results from parts (a) and (b). Apply the inequality max (f (x) + g (x)) c2) to both be 0.025. (If applicable, enter q(alpha) for qa the 1 - a-quantile of a standard normal distribution, e.g. enter q(0.01) for q0.01 ) C = cZ = Submit You have used 0 of 3 attempts Save (e) 2 points possible (graded) We will now show that the values we just derived for cj and cz are in fact too conservative. Recall the expression from part (b) for Pp(Xn 0.48 (note the strict inequality), find lim Pp (Xn 0.48Xn c2). Use the expression you found in part (b) for Pp(Xn > cz). lim Pp c>) = Submit You have used 0 of 3 attempts Save( 2 points possible {graded} Note: This part of the problem will contain multiple steps but you would only enter answers to the nal step. Also refer to the recitation 4 last video Composite Test for related ideas; Next. we analyze the asymptotic test given different possible values of p. in order to choose suitable and sufciently-tight c1 and oz Looking more closely at part {d}, we mayr note that the asymptotic behavior of the expressions for the errors are different depending on whether 11 = 0.43. 0.45