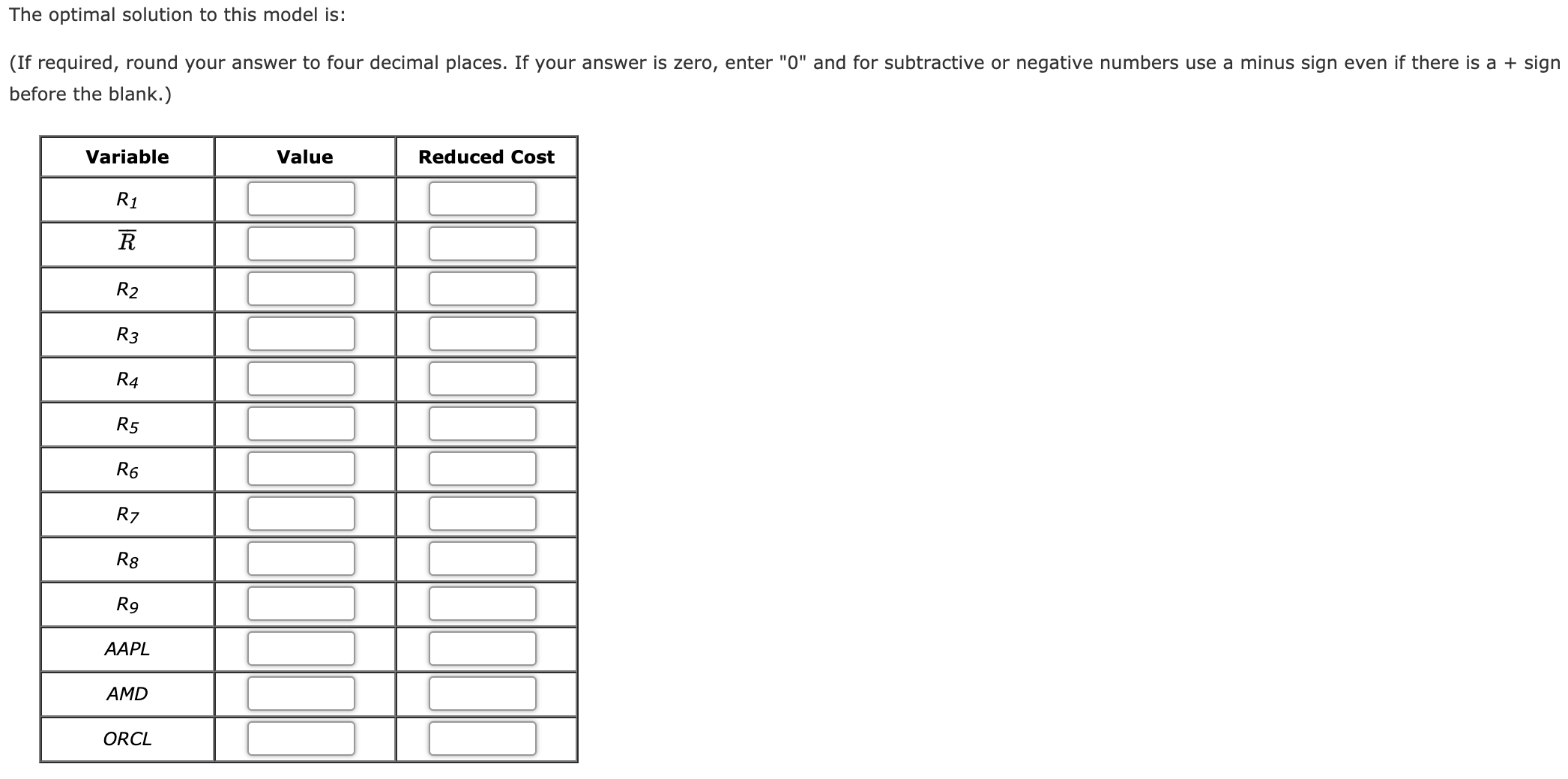
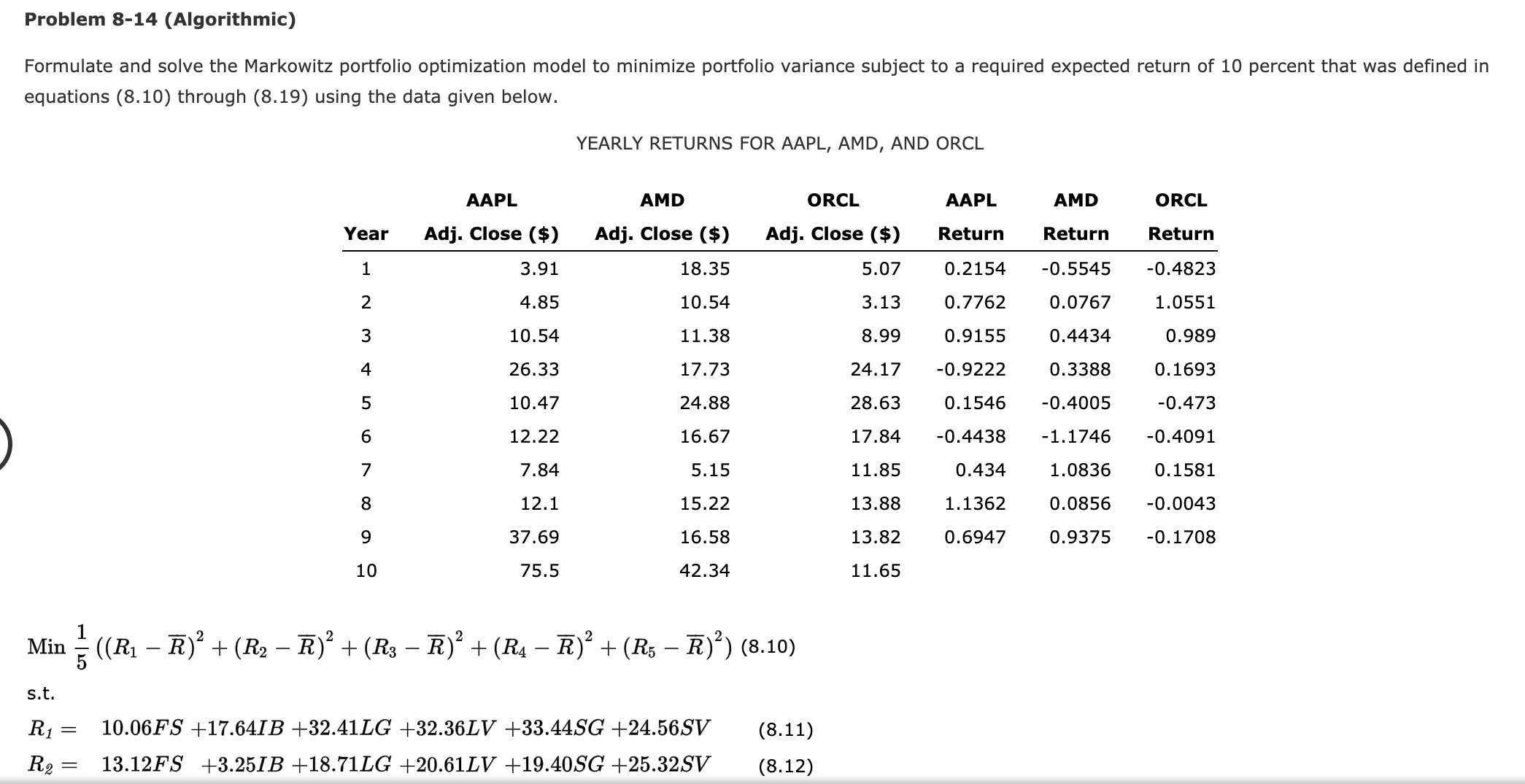
The question is stated below. All information is provided and none is missing.

Min ((R1 - R)' + (R2 - R) + ( R3 - R)2 + ( R4 - R) + ( Rs - R)?) (8.10) s.t. R1 = 10.06FS +17.641B +32.41LG +32.36LV +33.44SG +24.56SV (8.11) R2 = 13.12FS +3.25/B +18.71LG +20.61LV +19.40SG +25.32SV (8.12) R3 = 13.47FS +7.51/B +33.28LG +12.93LV +3.85SG -6.70SV (8.13) RA = 45.42FS -1.33/B +41.46LG +7.06LV +58.68SG +5.43SV (8.14) R5 = -21.93FS +7.361B -23.26LG -5.37LV -9.02SG +17.31SV (8.15) FS +IB +LG +LV +SG +SV = 1 (8.16) Ri+ R2+ Rg + R4 + R5 5 R (8.17) R > 10 (8.18) FS , IB , LG , LV , SG , SV 2 0 (8.19) In this case, nine scenarios correspond to the yearly returns from Year 1 through 9. Treat each scenario as being equally likely. If required, round your answer to four decimal places. If the constant is "1" it must be entered in the box. If your answer is negative value enter minus sign even if there is a + sign before the blank. Min v ((R1 - R)' + ( R2 - R)' + (R3 - R)' + ( RA - R)' + (R5 - R)' + ( Ro - R)' + ( R7 - R)' + ( Rg - R)' + ( Rg - R)?) AAPL + AMD + ORCL = R1 AAPL + AMD + ORCL = R2 AAPL + AMD + ORCL = R3The optimal solution to this model is: (If required, round your answer to four decimal places. If your answer is zero, enter "0" and for subtractive or negative numbers use a minus sign even if there is a + sign before the blank.) Variable Reduced Cost \\l U1 to N l.- In this case, nine scenarios correspond to the yearly returns from Year 1 through 9. Treat each scenario as being equally likely. If required, round your answer to four decimal places. If the constant is "1" it must be entered in the box. If your answer is negative value enter minus sign even if there is a + sign before the blank. Min v 9 ((R1 - R)' + (R2 - R)' + (R3 - R)' + (RA - R)' + ( R5 - R)' + ( R6 - R)' + ( R7 - R)' + ( Rg - R)' + ( Rg - R)' ) AAPL + AMD + ORCL = R1 AAPL + AMD + ORCL = R2 AAPL + AMD + ORCL = R3 AAPL + AMD + ORCL = R4 AAPL + AMD + ORCL = R5 AAPL + AMD + ORCL = R6 AAPL + AMD + ORCL = R7 AAPL + AMD + ORCL = R8 AAPL + AMD + ORCL = R9 AAPL + AMD + ORCL = 1 CO| H (R1 + R2 + R3 + R4 + R5 + R6 + R7 + R8 + Rg) = R R 0.1Problem 8-14 (Algorithmic) Formulate and solve the Markowitz portfolio optimization model to minimize portfolio variance subject to a required expected return of 10 percent that was defined in equations (8.10) through (8.19) using the data given below. YEARLY RETURNS FOR AAPL, AMD, AND ORCL AAPL AMD ORCL AAPL AMD ORCL Year Adj. Close ($) Adj. Close ($) Adj. Close ($) Return Return Return 3.91 18.35 5.07 0.2154 -0.5545 -0.4823 4.85 10.54 3.13 0.7762 0.0767 1.0551 10.54 11.38 8.99 0.9155 0.4434 0.989 26.33 17.73 24.17 -0.9222 0.3388 0.1693 10.47 24.88 28.63 0.1546 -0.4005 -0.473 12.22 16.67 17.84 -0.4438 -1.1746 -0.4091 7.84 5.15 11.85 0.434 1.0836 0.1581 12.1 15.22 13.88 1.1362 0.0856 -0.0043 37.69 16.58 13.82 0.6947 0.9375 -0.1708 10 75.5 42.34 11.65 Min = ((R1 - R)' + (R2 - R)' + ( R3 - R)' + ( R4 - R) + ( Rs - R)?) (8.10) s.t. R1 = 10.06FS +17.641B +32.41LG +32.36LV +33.44SG +24.56SV (8.11) R2 = 13.12FS +3.251B +18.71LG +20.61LV +19.40SG +25.32SV (8.12)