The questions are in the photos below: I would like them all solved, and the correct answers too.

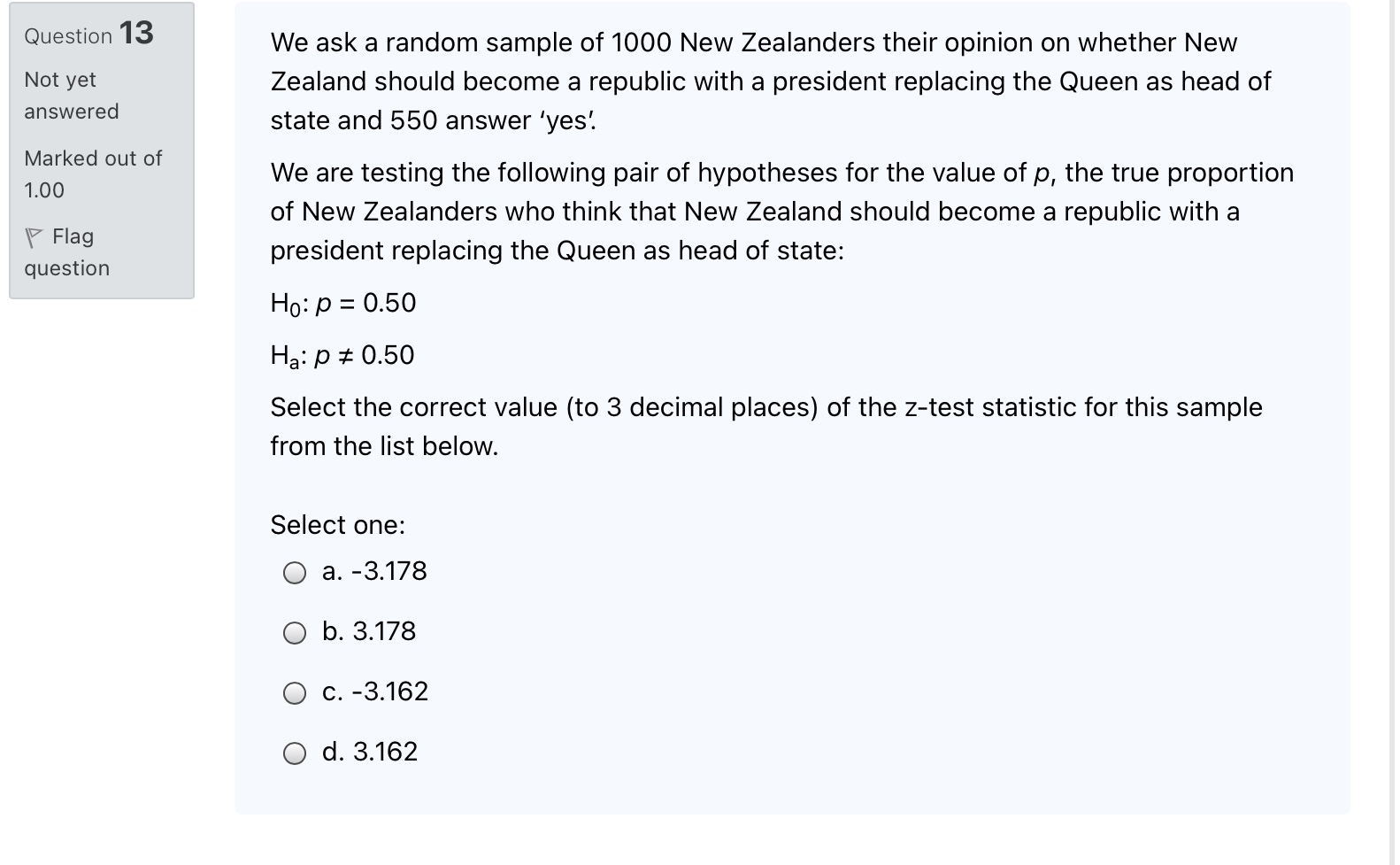
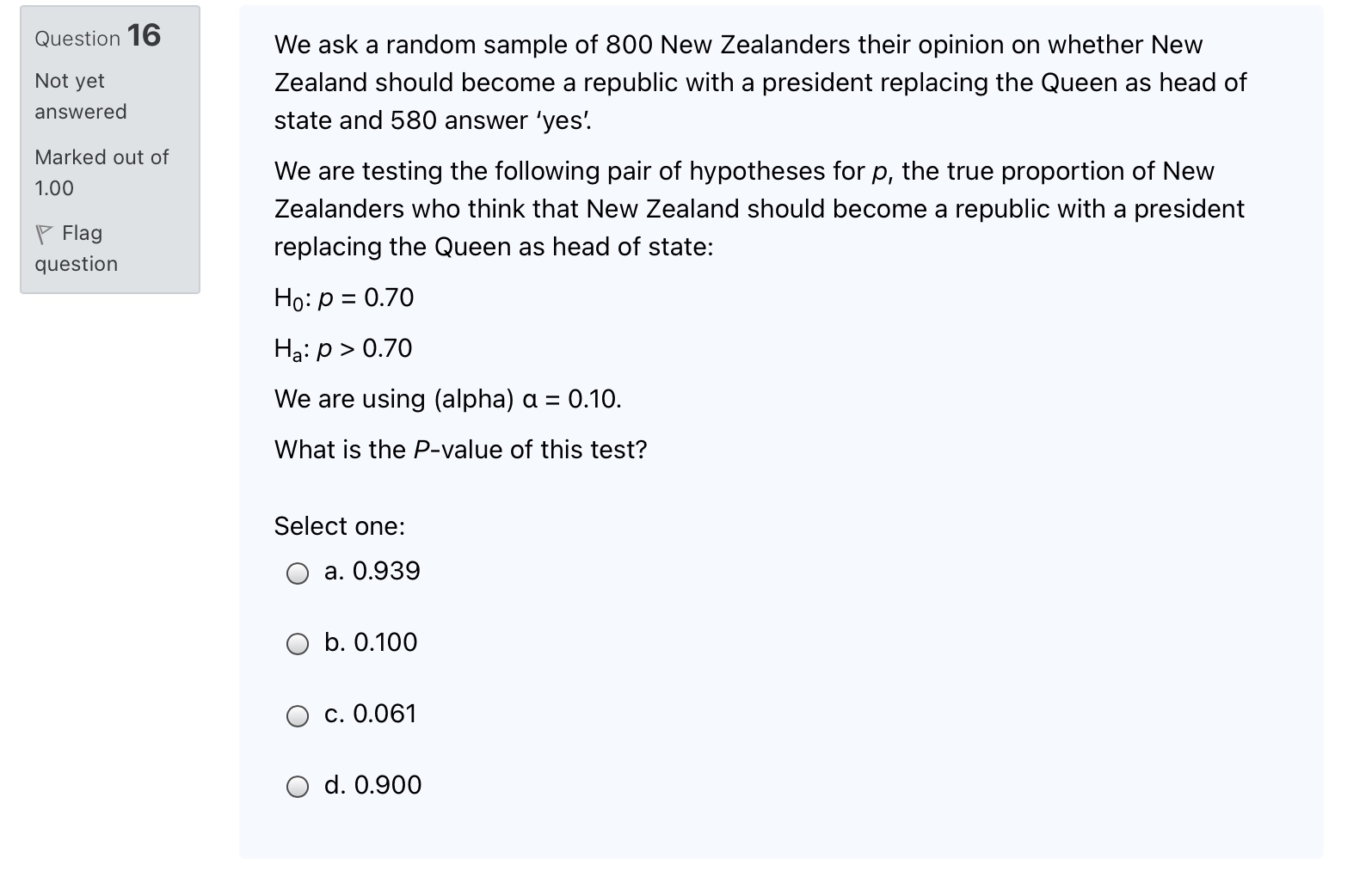
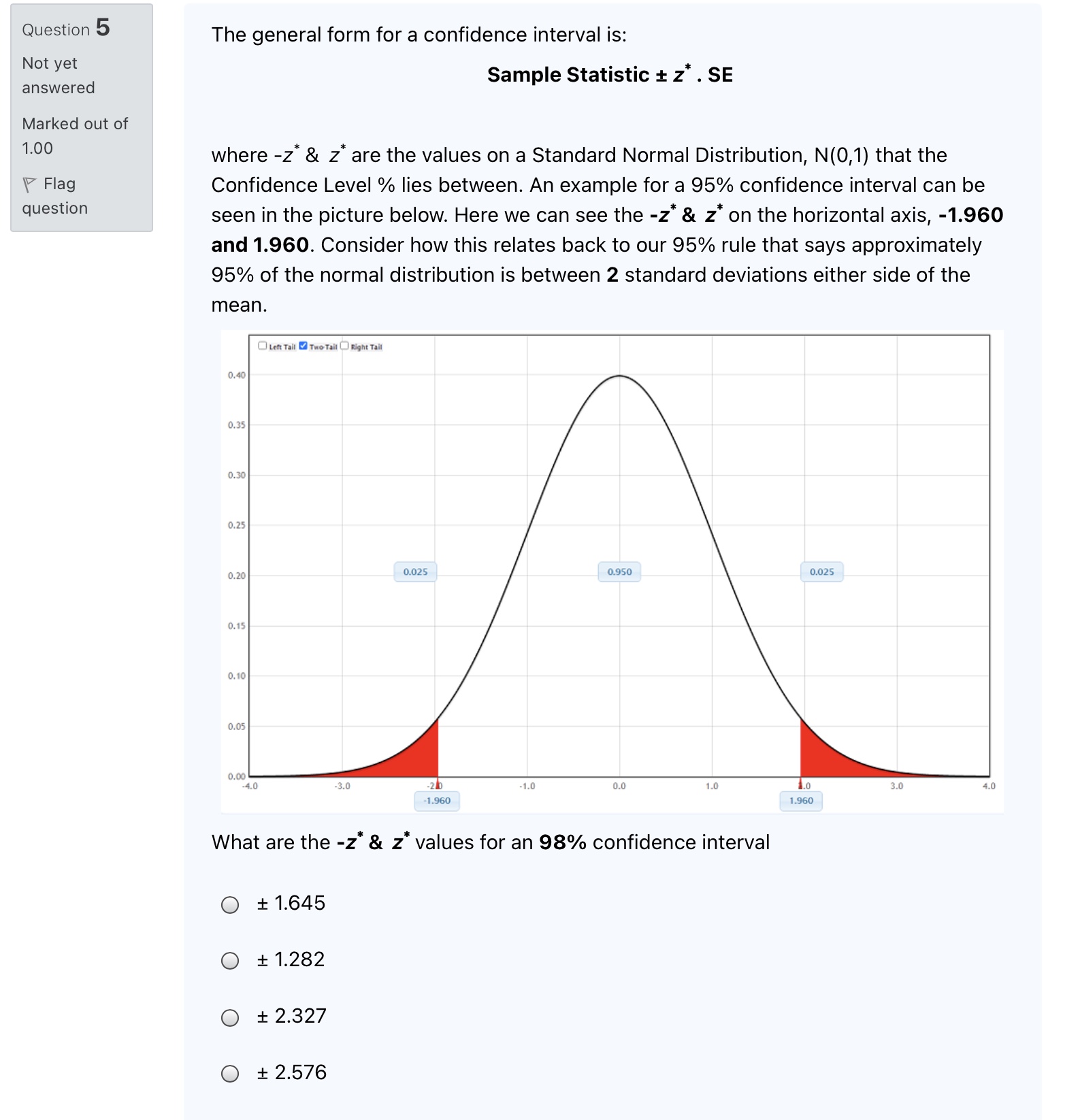
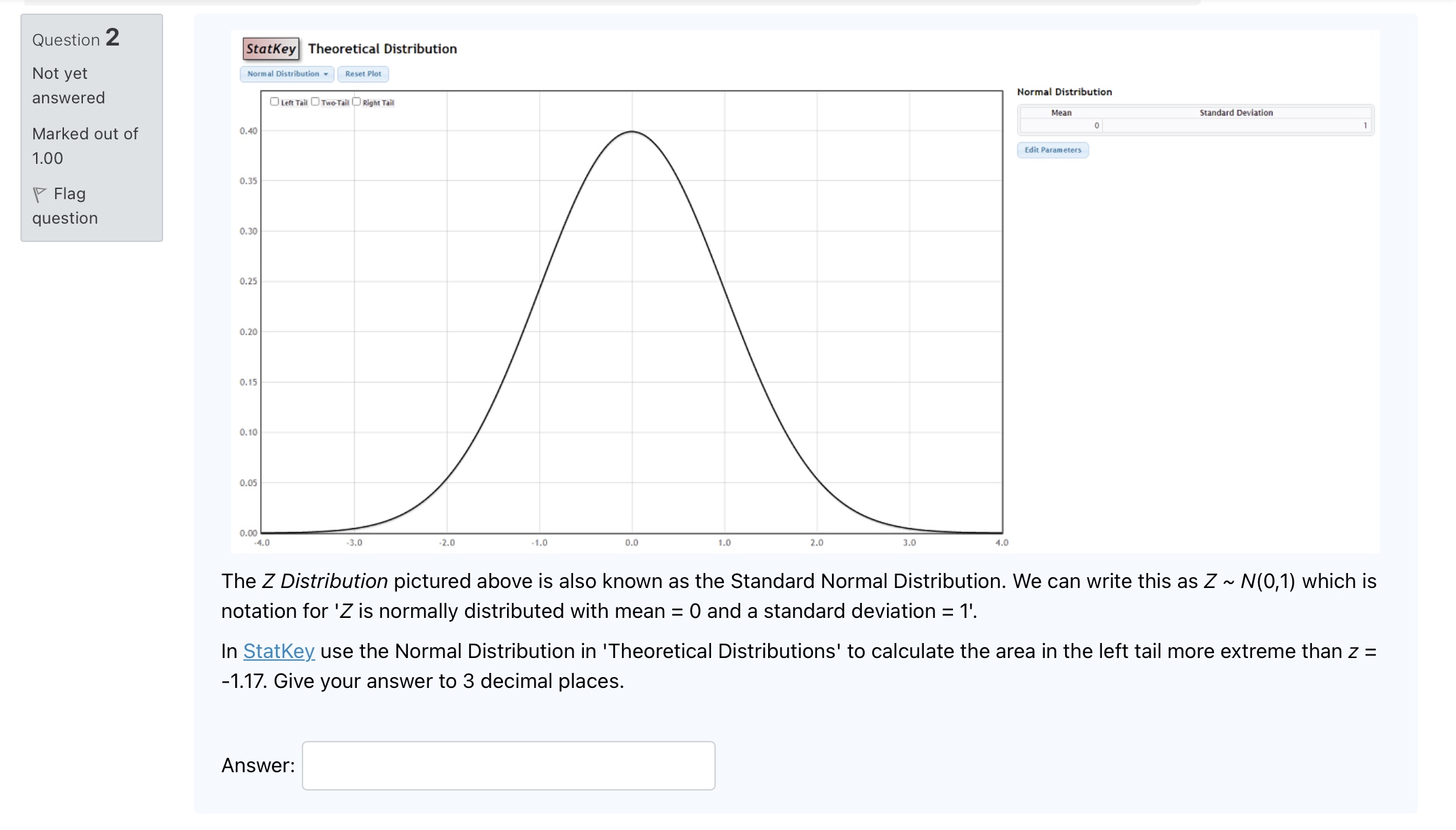
Question 15 Not yet answered Marked out of 1.00 1? Flag question We are performing a two-tailed hypothesis test for the value of a population proportion p using the following pair of hypotheses: Ho: p =O.43 vs. Ha: p i 0.43 We will test at (alpha) o = 0.10. After analysing the data we calculate the test statistic z = 1.581. What is the P-value for the test? Hint: consider the alternative hypothesis Ha carefully. Select one: o a. 0.114 0 b. 0.943 o c. 0.100 0 d. 0.057 Question 12 Not yet answered Marked out of 1.00 F Flag question A factory produces a component used in manufacturing computers. A sample of components is tested prior to shipment to determine how many defective components it contains. In a random sample of 313 components 54 were found to be defective. Using the method described in the Section 6.1 lecture notes, find the lower limit for the 95% confidence interval for the true proportion of defective components produced by the factory. Give your answer correct to 2 decimal places. Answer: Question 13 Not yet answered Marked out of 1.00 17 Flag question We ask a random sample of 1000 New Zealanders their opinion on whether New Zealand should become a republic with a president replacing the Queen as head of state and 550 answer 'yes'. We are testing the following pair of hypotheses for the value of p, the true proportion of New Zealanders who think that New Zealand should become a republic with a president replacing the Queen as head of state: Ho} p = 0.50 H3: ,0 at 0.50 Select the correct value {to 3 decimal places) of the ztest statistic for this sample from the list below. Select one: Q a. -3.'|78 O b. 3.178 O c. -3.162 Q d. 3.162 Question 3 Not yet answered Marked out of 1.00 F Flag question Use the hypotheses H0: u = 58.5 and Ha: u 0.70 We are using (alpha) d = 0.10. What is the P-value of this test? Select one: 0 a. 0.939 O b. 0.100 O C. 0.061 Q d. 0.900 QUESHO\" 7 In the construction of confidence intervals, if all other quantities are unchanged, a Not yet decrease in the sample size will lead to a interval. answered Marked out of Select one; 1.00 O a. Narrower V Flag question 0 b. Wider O c. Unchanged 0 d. Biased Question 17 Not yet answered Marked out of 1.00 '3' Flag question A factory produces a component used in manufacturing computers. The defect rate is supposed to be 0.05 (5%). A sample of components is tested prior to shipment to determine how many defective components it contains. In a random sample of 500 components, 15 were found to be defective. We are testing the following pair of hypotheses for the value of p, the true defect rate: Ho: p = 0.05 Ha: p :it 0.05 We are using (alpha) 0 = 0.01. What is the P-value of this test? Select one: Q a. 0.020 O b. 0.010 O c. 0.040 Q d. 0.980 Question 10 Not yet answered Marked out of 1.00 \\V Flag question The list below contains a number of statements about using confidence intervals of proportions. Select (tick) the only true statement in the list below. Select one: Q a. All other things being equalr a larger sample size will give us a larger confidence interval for a proportion. O b. We should check both the number of 'successes' in the sample and the number of 'failures' before we use confidence intervals on proportions. O c. We can calculate a confidence interval for a proportion whenever the sample size is n 2 30. Question 5 The general form for a confidence interval is: Not yet answered Sample Statistic + z* . SE Marked out of 1.00 where -z"& z" are the values on a Standard Normal Distribution, N(0,1) that the Flag Confidence Level % lies between. An example for a 95% confidence interval can be question seen in the picture below. Here we can see the -z & z* on the horizontal axis, -1.960 and 1.960. Consider how this relates back to our 95% rule that says approximately 95% of the normal distribution is between 2 standard deviations either side of the mean. O Left Tall Two Tall Right Tall 0.40 0.35 0.30 0.25 0.20 0.025 0.950 0.025 0.15 0.10 0.05 0.00 4.0 -3.0 -26 -1.0 0.0 1.0 3.0 -1.960 1.960 What are the -z' & z values for an 98% confidence interval O + 1.645 O + 1.282 O + 2.327 O + 2.576Question 9 Not yet answered Marked out of 1.00 V Flag question Suppose a confidence interval for a population mean turns out to be (1,000, 2,100) at the 90% confidence level. Suppose we repeat our calculation with a different sample size and confidence level. Which of the following changes we would expect to result in an increased interval width (select the option for 'None of these' if you do not think any of the suggested changes can be expected to give an increased confidence interval width). Select one: Q a. Changing the confidence level to 80%. O b. Doubling the sample size 0 c. Changing the confidence level to 99%. Q d. None of these. Question 2 StatKey Theoretical Distribution Not yet Normal Distribution . Reset Plot answered Normal Distribution OLeft Tail Two Tail Right Tail Mean Standard Deviation Marked out of 0.40 1.00 Edit Parameters 0.35 Flag question 0.30 0.25 0.20 0.15 0.10 0.05 0.00 .4.0 -3.0 -2.0 -1.0 0.0 1.0 2.0 3.0 The Z Distribution pictured above is also known as the Standard Normal Distribution. We can write this as Z ~ N(0,1) which is notation for 'Z is normally distributed with mean = 0 and a standard deviation = 1'. In Statkey use the Normal Distribution in 'Theoretical Distributions' to calculate the area in the left tail more extreme than z = -1.17. Give your answer to 3 decimal places. Answer:Question 1 Not yet answered Marked out of 1.00 '(7 Flag question Given the hypotheses Ho: [1 = 78.5 and Ha: u