The report should contain the foregoing, perhaps with a summary statement that generalises the usefulness of the model beyond the single case which is featured here. We can note also that a formula such as this can be used generally to check for errors in assigning Kchel numbers, by looking for wayward results when the formula is applied to large numbers of data. There should also be comment on reservations concerning precision, on account of approximations used in the approach.

Information in image.

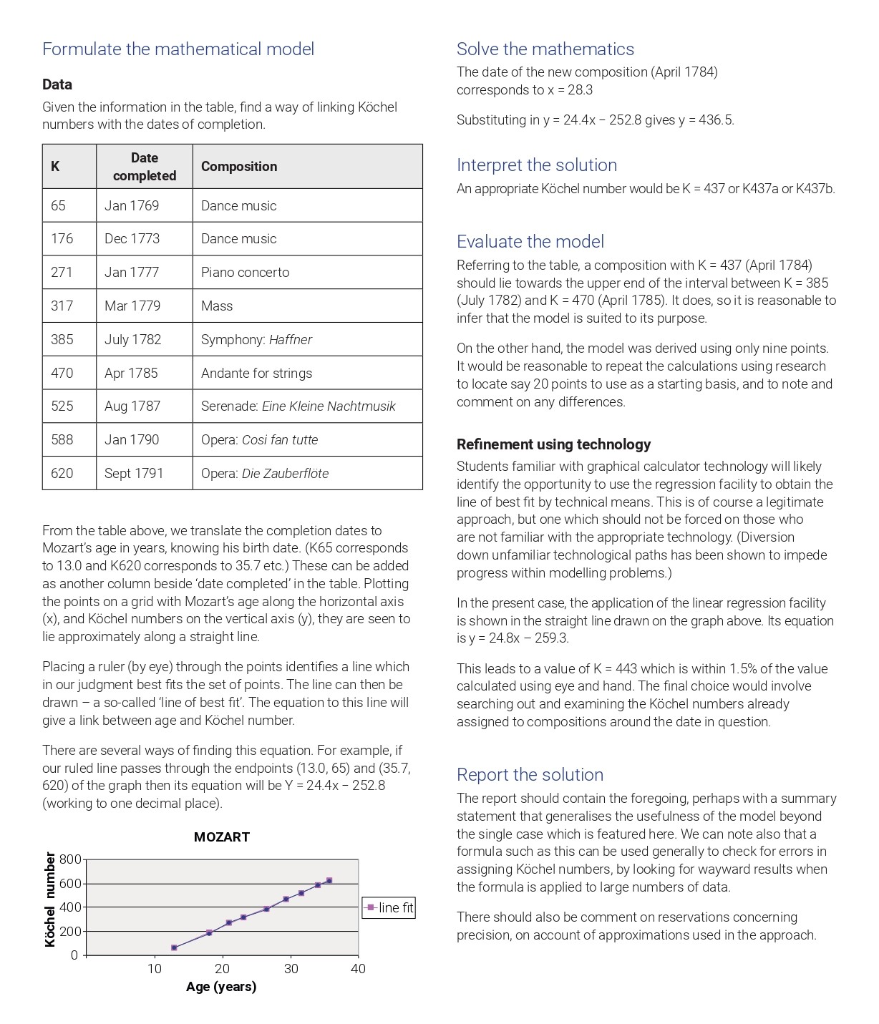
Kchel numbers Photo credit: Portrait of Mozart by Barbara Krafft Describe the real-world problem It is sobering to realise that when Mozart was my age he had already been dead for three years. Tom Lehrer, mathematician/comedian Wolfgang Amadeus Mozart, one of the most influential composers of the Classical era, was born January 27, 1756, in Salzburg, and died December 5, 1793, in Vienna. He composed more than 600 works over his career. Ludwig von Kchel, Viennese botanist, mineralogist and educator, published an inclusive, chronological catalogue of Mozart's work in 1862. Kchel (K) numbers are assigned sequentially according to the date of composition. For example, Mozart's opera The Magic Flute is given the Kchel number 620, and is (approximately) the 620th piece of music Mozart composed. Compositions completed at the same time are listed K69, K69a, and so on. Specify the mathematical problem A new composition by Mozart completed in April 1784 has come to light. What Kchel number should it be given? Formulate the mathematical model Solve the mathematics The date of the new composition (April 1784) corresponds to x = 28.3 Data Given the information in the table, find a way of linking Kchel numbers with the dates of completion. Substituting in y = 24.4x - 252.8 gives y = 436.5. K Date completed Composition Interpret the solution An appropriate Kchel number would be K = 437 or K437a or K437b. 65 Jan 1769 Dance music 176 Dec 1773 Dance music 271 Jan 1777 Piano concerto 317 Mar 1779 Mass Evaluate the model Referring to the table, a composition with K = 437 (April 1784) should lie towards the upper end of the interval between K = 385 (July 1782) and K = 470 (April 1785). It does, so it is reasonable to infer that the model is suited to its purpose. On the other hand, the model was derived using only nine points. It would be reasonable to repeat the calculations using research to locate say 20 points to use as a starting basis, and to note and comment on any differences. 385 July 1782 Symphony: Haffner 470 Apr 1785 Andante for strings 525 Aug 1787 Serenade: Eine Kleine Nachtmusik 588 Jan 1790 Opera: Cosi fan tutte 620 Sept 1791 Opera: Die Zauberflote From the table above, we translate the completion dates to Mozart's age in years, knowing his birth date. (K65 corresponds to 13.0 and K620 corresponds to 35.7 etc.) These can be added as another column beside 'date completed' in the table. Plotting the points on a grid with Mozart's age along the horizontal axis (x), and Kchel numbers on the vertical axis (y), they are seen to lie approximately along a straight line. Placing a ruler (by eye) through the points identifies a line which in our judgment best fits the set of points. The line can then be drawn - a so-called 'line of best fit'. The equation to this line will give a link between age and Kochel number Refinement using technology Students familiar with graphical calculator technology will likely identify the opportunity to use the regression facility to obtain the line of best fit by technical means. This is of course a legitimate approach, but one which should not be forced on those who are not familiar with the appropriate technology. (Diversion down unfamiliar technological paths has been shown to impede progress within modelling problems.) In the present case, the application of the linear regression facility is shown in the straight line drawn on the graph above. Its equation is y = 24.8x - 2593 This leads to a value of K = 443 which is within 1.5% of the value calculated using eye and hand. The final choice would involve searching out and examining the Kchel numbers already assigned to compositions around the date in question. There are several ways of finding this equation. For example, if our ruled line passes through the endpoints (13.0, 65) and (35.7 620) of the graph then its equation will be Y = 24.4x - 252.8 (working to one decimal place). MOZART 800 Report the solution The report should contain the foregoing, perhaps with a summary statement that generalises the usefulness of the model beyond the single case which is featured here. We can note also that a formula such as this can be used generally to check for errors in assigning Kchel numbers, by looking for wayward results when the formula is applied to large numbers of data. There should also be comment on reservations concerning precision, on account of approximations used in the approach. 600 Kchel number 400 +-line fit 200 0 10 30 40 20 Age (years) Kchel numbers Photo credit: Portrait of Mozart by Barbara Krafft Describe the real-world problem It is sobering to realise that when Mozart was my age he had already been dead for three years. Tom Lehrer, mathematician/comedian Wolfgang Amadeus Mozart, one of the most influential composers of the Classical era, was born January 27, 1756, in Salzburg, and died December 5, 1793, in Vienna. He composed more than 600 works over his career. Ludwig von Kchel, Viennese botanist, mineralogist and educator, published an inclusive, chronological catalogue of Mozart's work in 1862. Kchel (K) numbers are assigned sequentially according to the date of composition. For example, Mozart's opera The Magic Flute is given the Kchel number 620, and is (approximately) the 620th piece of music Mozart composed. Compositions completed at the same time are listed K69, K69a, and so on. Specify the mathematical problem A new composition by Mozart completed in April 1784 has come to light. What Kchel number should it be given? Formulate the mathematical model Solve the mathematics The date of the new composition (April 1784) corresponds to x = 28.3 Data Given the information in the table, find a way of linking Kchel numbers with the dates of completion. Substituting in y = 24.4x - 252.8 gives y = 436.5. K Date completed Composition Interpret the solution An appropriate Kchel number would be K = 437 or K437a or K437b. 65 Jan 1769 Dance music 176 Dec 1773 Dance music 271 Jan 1777 Piano concerto 317 Mar 1779 Mass Evaluate the model Referring to the table, a composition with K = 437 (April 1784) should lie towards the upper end of the interval between K = 385 (July 1782) and K = 470 (April 1785). It does, so it is reasonable to infer that the model is suited to its purpose. On the other hand, the model was derived using only nine points. It would be reasonable to repeat the calculations using research to locate say 20 points to use as a starting basis, and to note and comment on any differences. 385 July 1782 Symphony: Haffner 470 Apr 1785 Andante for strings 525 Aug 1787 Serenade: Eine Kleine Nachtmusik 588 Jan 1790 Opera: Cosi fan tutte 620 Sept 1791 Opera: Die Zauberflote From the table above, we translate the completion dates to Mozart's age in years, knowing his birth date. (K65 corresponds to 13.0 and K620 corresponds to 35.7 etc.) These can be added as another column beside 'date completed' in the table. Plotting the points on a grid with Mozart's age along the horizontal axis (x), and Kchel numbers on the vertical axis (y), they are seen to lie approximately along a straight line. Placing a ruler (by eye) through the points identifies a line which in our judgment best fits the set of points. The line can then be drawn - a so-called 'line of best fit'. The equation to this line will give a link between age and Kochel number Refinement using technology Students familiar with graphical calculator technology will likely identify the opportunity to use the regression facility to obtain the line of best fit by technical means. This is of course a legitimate approach, but one which should not be forced on those who are not familiar with the appropriate technology. (Diversion down unfamiliar technological paths has been shown to impede progress within modelling problems.) In the present case, the application of the linear regression facility is shown in the straight line drawn on the graph above. Its equation is y = 24.8x - 2593 This leads to a value of K = 443 which is within 1.5% of the value calculated using eye and hand. The final choice would involve searching out and examining the Kchel numbers already assigned to compositions around the date in question. There are several ways of finding this equation. For example, if our ruled line passes through the endpoints (13.0, 65) and (35.7 620) of the graph then its equation will be Y = 24.4x - 252.8 (working to one decimal place). MOZART 800 Report the solution The report should contain the foregoing, perhaps with a summary statement that generalises the usefulness of the model beyond the single case which is featured here. We can note also that a formula such as this can be used generally to check for errors in assigning Kchel numbers, by looking for wayward results when the formula is applied to large numbers of data. There should also be comment on reservations concerning precision, on account of approximations used in the approach. 600 Kchel number 400 +-line fit 200 0 10 30 40 20 Age (years)