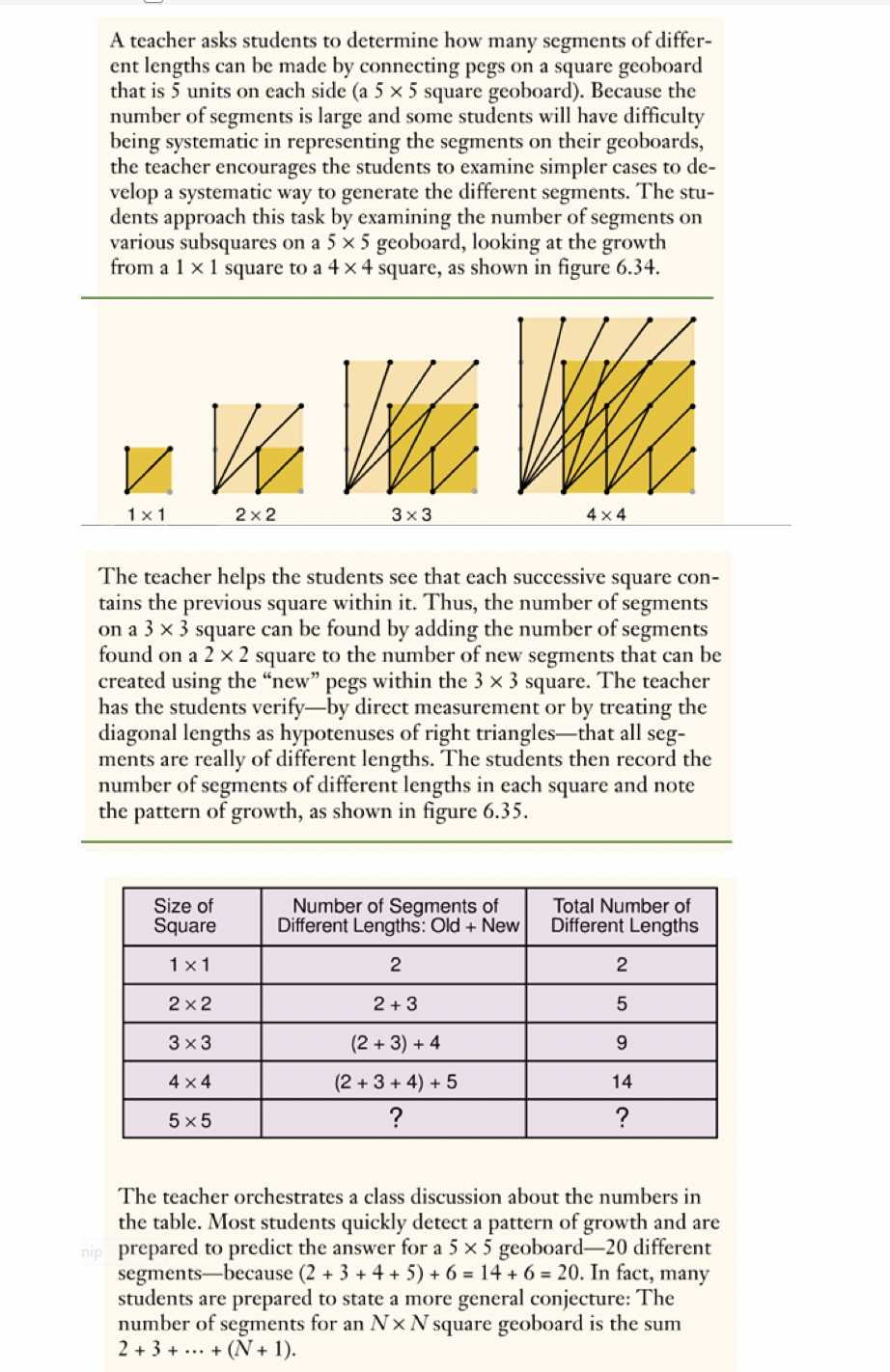
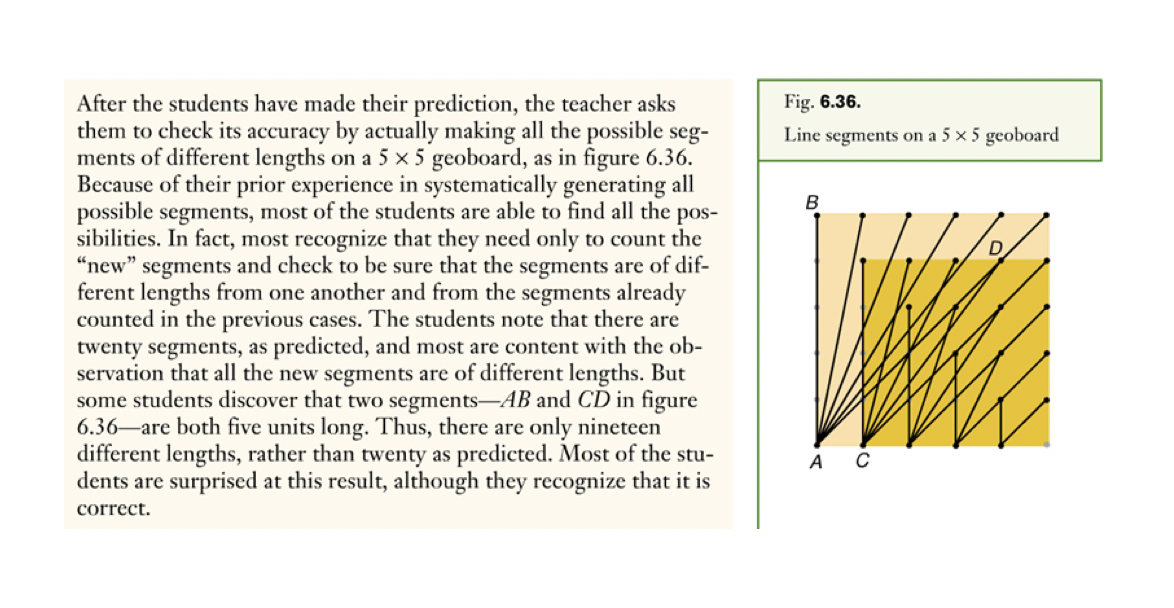
The Role of Examples in Proof: Read "Proof: Examples and Beyond" in D2L. Respond to the following questions. 1. What is the difficulty with a "proof" by example? 2. When is a proof by example acceptable? 3. Examples are often helpful in forming conjectures which may or may not be true. The segment lengths problem below is the one to which the authors refer (from Principles and Standards for School Mathematics). Examine the problem and the exposition of it in the classroom. Based on the article, why is this kind of problem important for students to explore? 4. Referring to the segment lengths problem, what are the implications for teacher learning? In other words, what must a teacher know and be able to do in order to help students develop the ability to reason mathematically and to justify their reasoning? A teacher asks students to determine how many segments of differ- ent lengths can be made by connecting pegs on a square geoboard that is 5 units on each side (a 5 x 5 square geoboard). Because the number of segments is large and some students will have difficulty being systematic in representing the segments on their geoboards, the teacher encourages the students to examine simpler cases to de- velop a systematic way to generate the different segments. The stu- dents approach this task by examining the number of segments on various subsquares on a 5 x 5 geoboard, looking at the growth from a 1 x 1 square to a 4 x 4 square, as shown in figure 6.34. 1 x 1 2 x 2 3x3 4 X 4 The teacher helps the students see that each successive square con- tains the previous square within it. Thus, the number of segments on a 3 x 3 square can be found by adding the number of segments found on a 2 x 2 square to the number of new segments that can be created using the new pegs within the 3 x 3 square. The teacher has the students verifyby direct measurement or by treating the diagonal lengths as hypotenuses of right trianglesthat all seg- ments are really of different lengths. The students then record the number of segments of different lengths in each square and note the pattern of growth, as shown in figure 6.35. Size of Square Number of Segments of Different Lengths: Old + New Total Number of Different Lengths 2 5 1x1 2x2 3x3 4x4 5x5 9 2+3 (2+ 3) + 4 (2+ 3+ 4) + 5 ? nip The teacher orchestrates a class discussion about the numbers in the table. Most students quickly detect a pattern of growth and are prepared to predict the answer for a 5 x 5 geoboard20 different segments-because (2 + 3 + 4 + 5) + 6 = 14 + 6 = 20. In fact, many students are prepared to state a more general conjecture: The number of segments for an Nx N square geoboard is the sum 2 + 3 + ... + (N+1). Fig. 6.36. Line segments on a 5 x 5 geoboard After the students have made their prediction, the teacher asks them to check its accuracy by actually making all the possible seg- ments of different lengths on a 5 x 5 geoboard, as in figure 6.36. Because of their prior experience in systematically generating all possible segments, most of the students are able to find all the pos- sibilities. In fact, most recognize that they need only to count the "new" segments and check to be sure that the segments are of dif- ferent lengths from one another and from the segments already counted in the previous cases. The students note that there are twenty segments, as predicted, and most are content with the ob- servation that all the new segments are of different lengths. But some students discover that two segments-AB and CD in figure 6.36are both five units long. Thus, there are only nineteen different lengths, rather than twenty as predicted. Most of the stu- dents are surprised at this result, although they recognize that it is correct