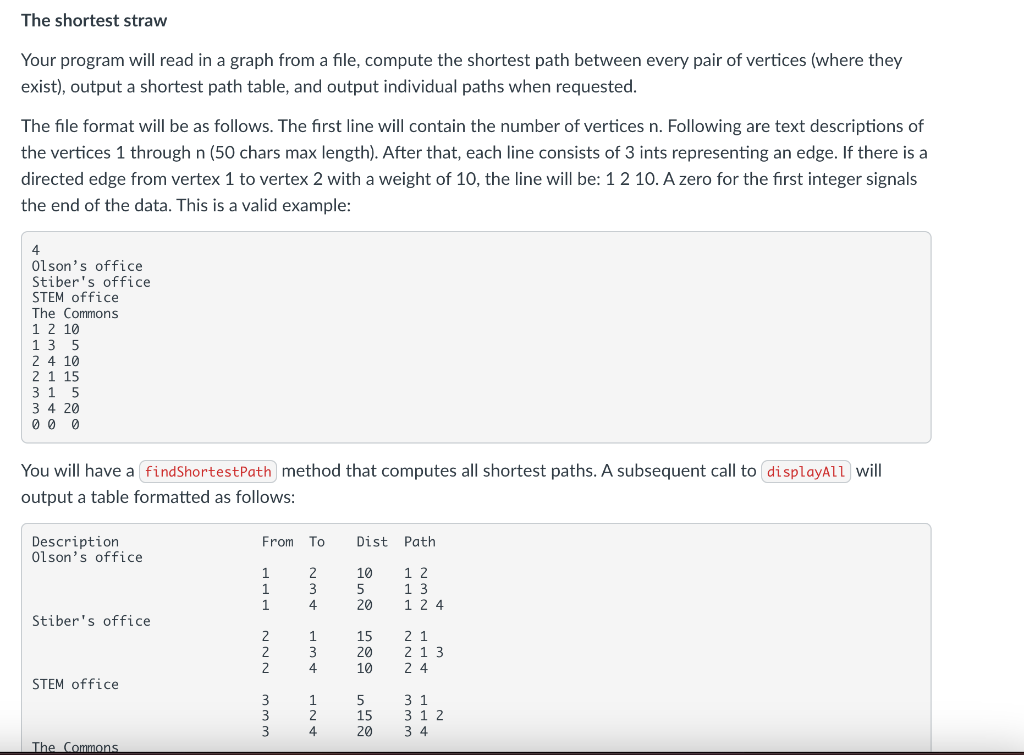
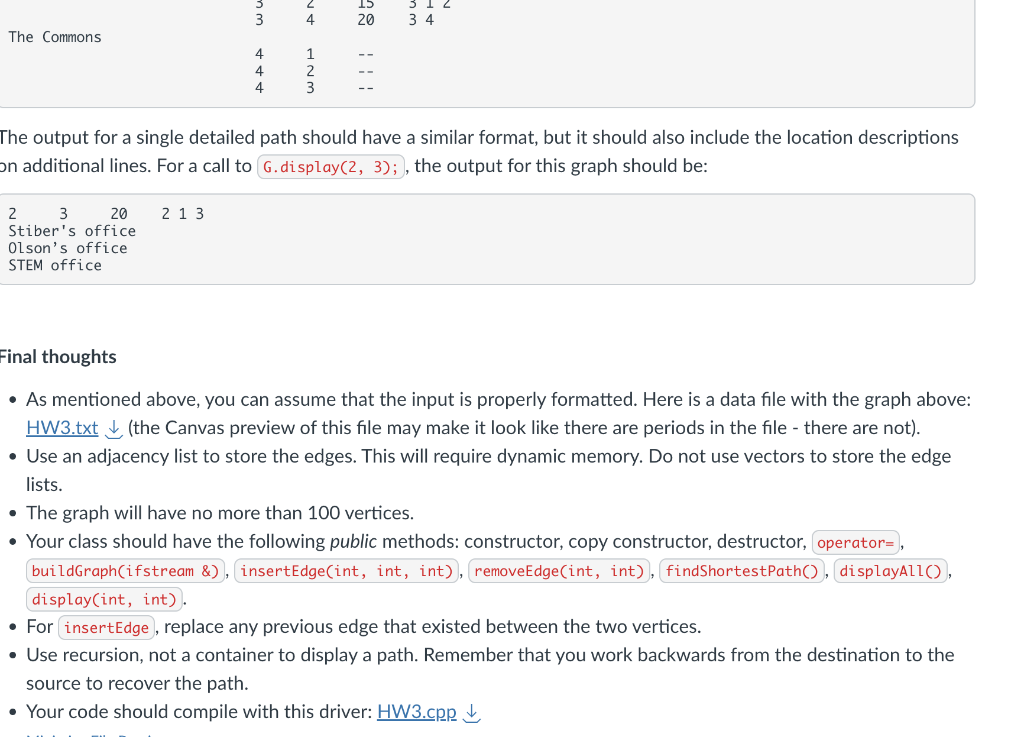
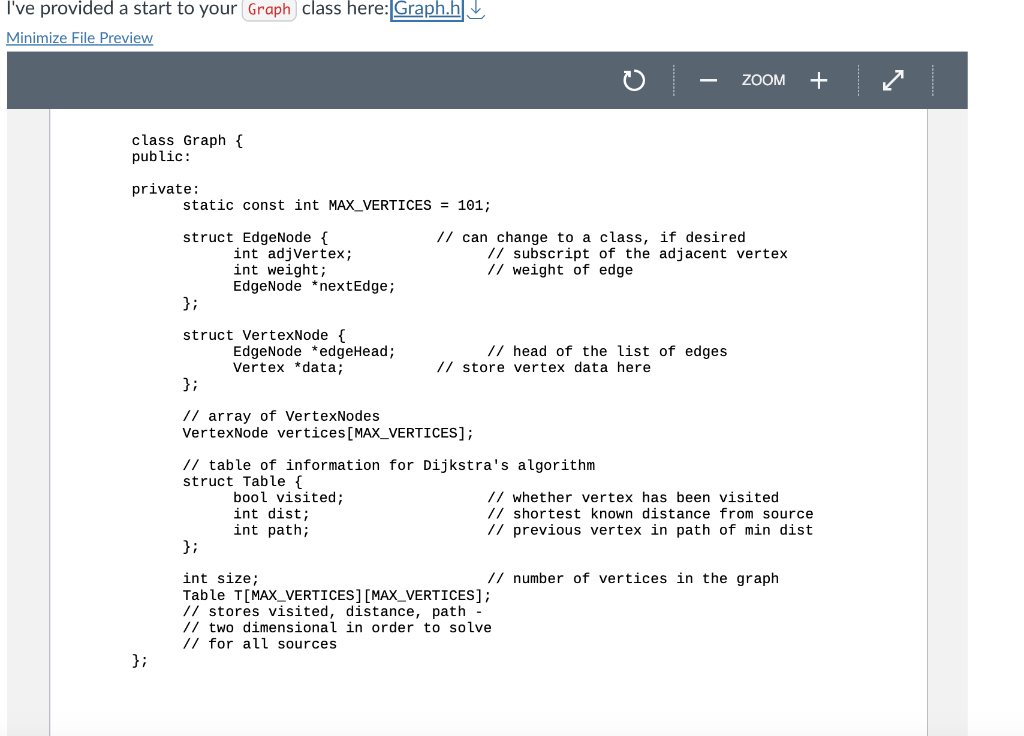
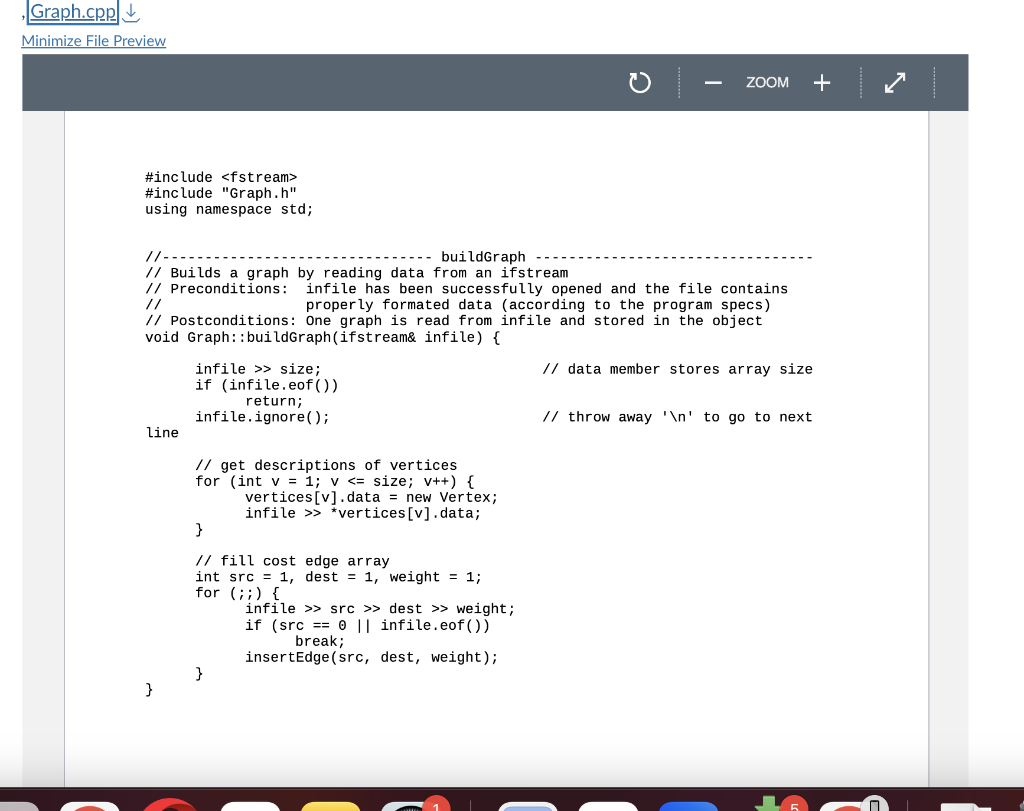
The shortest straw Your program will read in a graph from a file, compute the shortest path between every pair of vertices (where they exist), output a shortest path table, and output individual paths when requested. The file format will be as follows. The first line will contain the number of vertices n. Following are text descriptions of the vertices 1 through n ( 50 chars max length). After that, each line consists of 3 ints representing an edge. If there is a directed edge from vertex 1 to vertex 2 with a weight of 10 , the line will be: 1210 . A zero for the first integer signals the end of the data. This is a valid example: 4 Olson's office Stiber's office STEM office The Commons 1122330234114010510155200 You will have a method that computes all shortest paths. A subsequent call to will output a table formatted as follows: The output for a single detailed path should have a similar format, but it should also include the location descriptions additional lines. For a call to , the output for this graph should be: Final thoughts - As mentioned above, you can assume that the input is properly formatted. Here is a data file with the graph above: (the Canvas preview of this file may make it look like there are periods in the file - there are not). - Use an adjacency list to store the edges. This will require dynamic memory. Do not use vectors to store the edge lists. - The graph will have no more than 100 vertices. - Your class should have the following public methods: constructor, copy constructor, destructor, - For , replace any previous edge that existed between the two vertices. - Use recursion, not a container to display a path. Remember that you work backwards from the destination to the source to recover the path. - Your code should compile with this driver: I've provided a start to your class here: Minimize File Preview \} - You should write a simple class that stores the description in private data and that includes (at least) and . (Hint: use to make easy.) - The header file provides you with a struct like in the notes and a 2D array of elements, which is necessary to record all shortest paths (not just a single source). - At each step of Dijkstra's algorithm, you will need to determine which vertex to visit next. The best way to accomplish this is using a priority queue (heap). However, I recommend starting with a less efficient technique that scans the entire array of vertices for the unvisited vertex with the lowest weight path. This results in an O(n2) algorithm for a single source (if done correctly). You will run the algorithm using each vertex as the source. - When you have a working algorithm, transition your code to use either the PriorityQueue class from Program 2 or the STL priority_queue class. Zelevant module goals - Be able to implement shortest path algorithms in unweighted and positive-weighted directed graphs using either adjacency matrices or adjacency lists