the solution of this should be in R programming even though it will be in hand writing
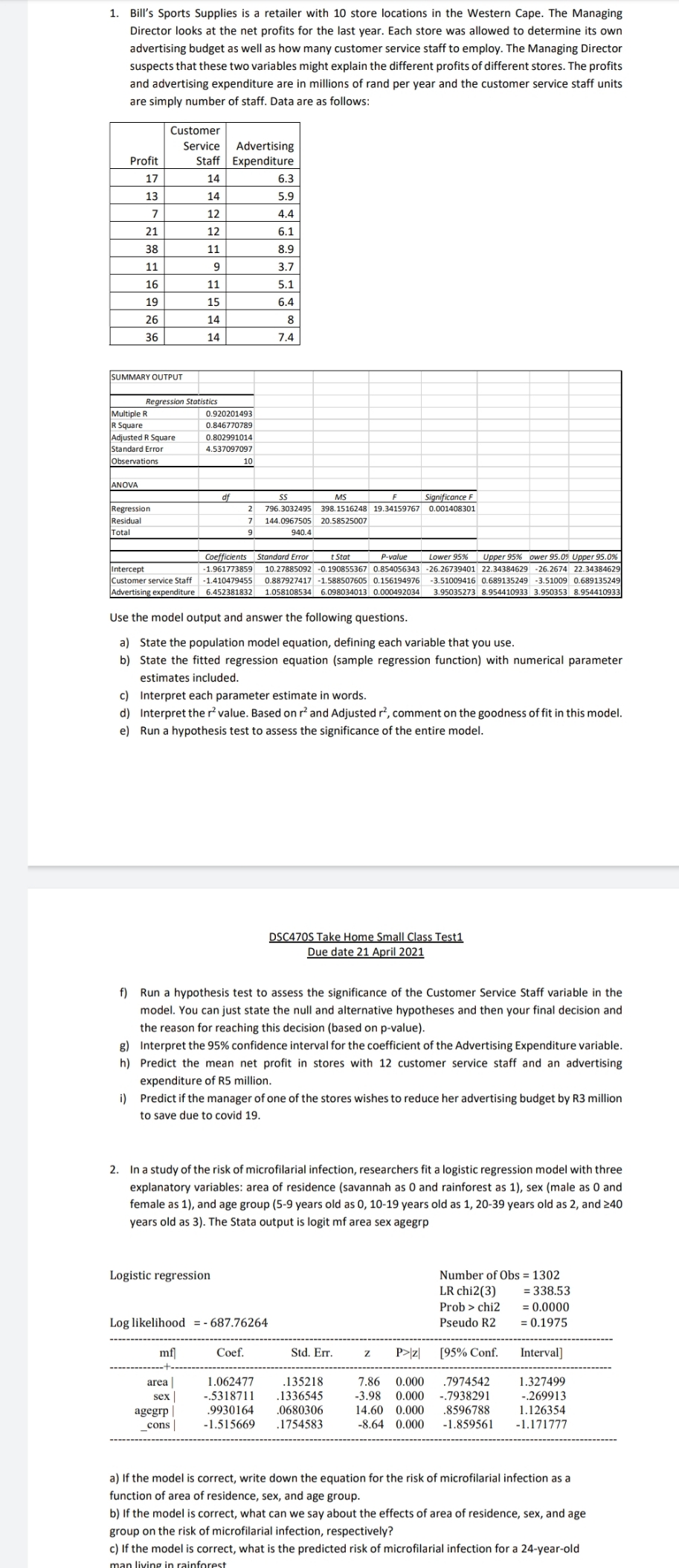
1. Bill's Sports Supplies is a retailer with 10 store locations in the Western Cape. The Managing Director looks at the net profits for the last year. Each store was allowed to determine its own advertising budget as well as how many customer service staff to employ. The Managing Director suspects that these two variables might explain the different profits of different stores. The profits and advertising expenditure are in millions of rand per year and the customer service staff units are simply number of staff. Data are as follows: Customer Service Advertising Profit Staff Expenditure 17 14 6.3 13 14 5.9 7 12 4.4 21 12 6.1 38 11 8.9 11 9 3.7 16 11 5.1 19 15 6.4 26 14 8 36 14 7.4 SUMMARY OUTPUT Regression Statistics Multiple R 0.920201493 R Square 0.846770789 Adjusted R Square 0.802991014 Standard Error 4.537097097 Observations 10 ANOVA SS MS Significance F Regression 2 796.3032495 398.1516248 19.34159767 0.001408301 Residual 7 144.0967505 20.58525007 Total 940.4 Coefficients P-value Lower 95% Upper 95% ower 95.09 Upper 95.0% Intercept -1.961773859 10.27885092 -0.190855367 0.854056343 -26.26739401 22.34384629 -26.2674 22.34384629 Customer service Staff -1.410479455 0.887927417 -1.588507605 0.156194976 -3.51009416 0.689135249 -3.51009 0.689135249 Advertising expen 3 0.000492034 3.95035273 8.954410933 3.950353 8.954410933 Use the model output and answer the following questions. a) State the population model equation, defining each variable that you use. b) State the fitted regression equation (sample regression function) with numerical parameter estimates included. c) Interpret each parameter estimate in words. d) Interpret the r value. Based on r and Adjusted r, comment on the goodness of fit in this model. e) Run a hypothesis test to assess the significance of the entire model. DSC470S Take Home Small Class Test1 Due date 21 April 2021 f) Run a hypothesis test to assess the significance of the Customer Service Staff variable in the model. You can just state the null and alternative hypotheses and then your final decision and the reason for reaching this decision (based on p-value) g) Interpret the 95% confidence interval for the coefficient of the Advertising Expenditure variable. h) Predict the mean net profit in stores with 12 customer service staff and an advertising expenditure of R5 million. i) Predict if the manager of one of the stores wishes to reduce her advertising budget by R3 million to save due to covid 19. 2. In a study of the risk of microfilarial infection, researchers fit a logistic regression model with three explanatory variables: area of residence (savannah as 0 and rainforest as 1), sex (male as 0 and female as 1), and age group (5-9 years old as 0, 10-19 years old as 1, 20-39 years old as 2, and 240 years old as 3). The Stata output is logit mf area sex agegrp Logistic regression Number of Obs = 1302 LR chi2(3) = 338.53 Prob > chi2 = 0.0000 Log likelihood = - 687.76264 Pseudo R2 = 0.1975 mf Coef. Std. Err. P>/z) [95% Conf. Interval] area 1.062477 .135218 7.86 0.000 7974542 1.327499 sex .5318711 .1336545 -3.98 .7938291 -.269913 agegrp .9930164 .0680306 14.60 0.000 8596788 1.126354 cons -1.515669 1754583 -8.64 0.000 -1.859561 -1.171777 a) If the model is correct, write down the equation for the risk of microfilarial infection as a function of area of residence, sex, and age group b) If the model is correct, what can we say about the effects of area of residence, sex, and age group on the risk of microfilarial infection, respectively? c) If the model is correct, what is the predicted risk of microfilarial infection for a 24-year-old