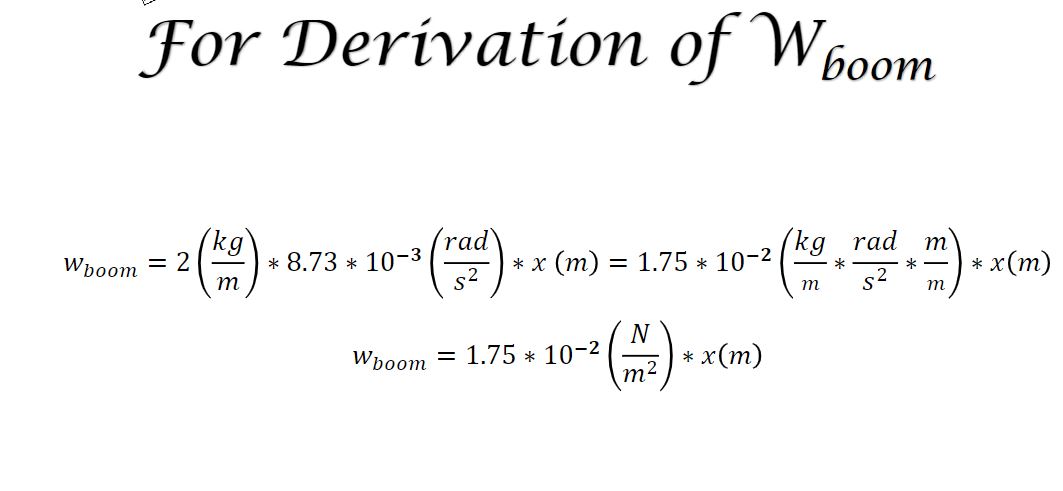
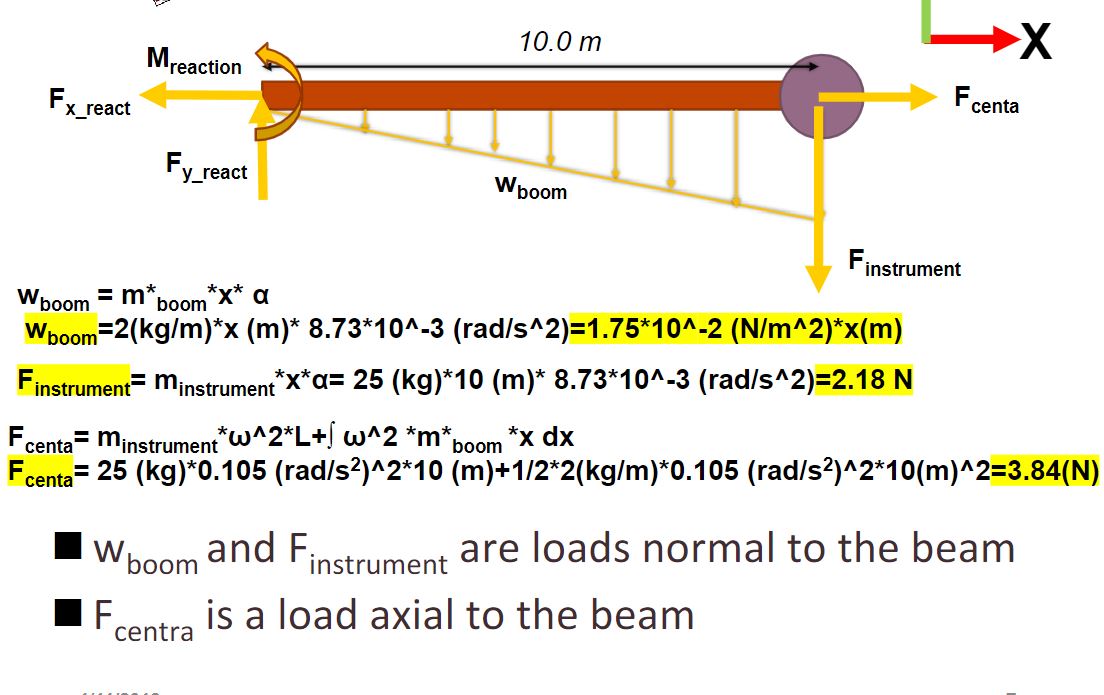
The spacecraft rotates in the plane of the paper Max angular velocity is 1 rpm Max angular acceleration is 5 rpm^2 Assume the beam is a cylinder with a diameter of 10mm. 10.0 m Y Spacecraft X m* boom = 2 kg/m Z minstrument 25 kg Find the maximum (absolute) principle stresses in the beam (35%) Identify where in the beam the stress is maximum. Requires combining any of the relevant stresses, possibly including transverse shear, bending and normal stress. Ensure this includes all forces and loads in the diagram below. For Derivation of We boom =2() + 8.73 + 10- () + x (m) = 1.75 + 10-()+x(m) N Wboom 1.75 * 10-2 *x(m) m _react Mreaction 10.0 m F centa y_react W boom Finstrument X Wboom =m* *x* a boom Wboom=2(kg/m)*x (m)* 8.73*10^-3 (rad/s^2)=1.75*10^-2 (N/m^2)*x(m) Finstrument minstrument *x*= 25 (kg)*10 (m)* 8.73*10^-3 (rad/s^2)=2.18 N F centa = minstrument *w^2*L+ w^2 *m* boom *x dx centa= 25 (kg)*0.105 (rad/s)^2*10 (m)+1/2*2(kg/m)*0.105 (rad/s)^2*10(m)^2=3.84(N) W boom and Finstrument are loads normal to the beam F centra is a load axial to the beam We need to convert RPM to rad/s Max angular velocity is 1 rpm 1*(2*pi)*(1/(60)=0.105rad/s Max angular acceleration is 5 rpm 5*(2*pi)*(1/(60*60)=8.73*10^-3 rad/s