The success average of a hockey player is the number of “points scored” divided by the number of “shots on goal.” Recently, a certain professional league player’s shots on goal and corresponding points scored were recorded for 400 consecutive games. The consecutive games span more than one season. Since each game is different, the number of shots and points scored both vary. For this particular player, there were from 0 to 15 shots. Thus, one can sort the more than 400 games into 16 categories: 0 shots 1 shot 2 shots . . . 14 shots 15 shots.

Consider the games where the player had exactly five shots on goal. A similar analysis can be done for each of the other shots category. Download the file titled Hockey. It contains a scatter plot of the Five Shots number of successes versus frequency. To compare the results to the Binomial Distribution, complete the following:

1. From the frequency distribution, construct the corresponding probability distribution. Explain why it is a probability distribution. Then, use Excel to make a scatter plot of the probability distribution: Select the two columns of the probability distribution.

2. Using the frequency distribution, what is the player’s success average for five shots? In part 3, note that the numerator in the formula for the mean is the total number of successes. The total number of shots is the denominator of the formula for the mean multiplied by 5.

3. The Binomial Distribution is uniquely determined by n, the number of trials, and p, the probability of “success” on each trial. Using Excel, construct the Binomial Probability Distribution for five trials, n, and probability of success, p, as the success average in part 5. Here is an explanation of the BINOM.DIST function (Links to an external site.)Links to an external site. in Excel For example, In Excel =BINOM.DIST(7,15,0.7,FALSE) represents the probability of 7 successes out of 15 (n) trials. The 0.7 is the probability of success, p.

4. Using the formula for the mean of the binomial distribution, what is the mean number of successes in part 6 up above?

5. In Excel, make a scatter plot for the binomial distribution. The instructions for making one are in part 4 up above.

6. Use the results up above to compare the probability distribution of five shots and the Binomial Distribution. Compare the means in parts 4 and 6, too. If the probability distribution of five shots and the Binomial Distribution differ, explain why that is so.

 

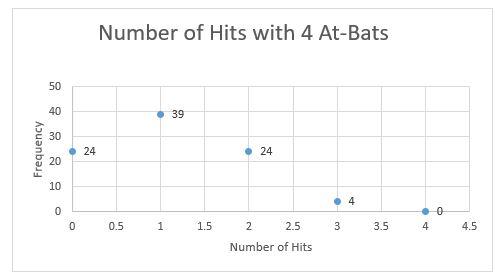
Frequency 50 40 30 20 10 0 0 24 Number of Hits with 4 At-Bats 0.5 1 39 1.5 24 2 2.5 Number of Hits -. 3 4 3.5 4 0 4.5