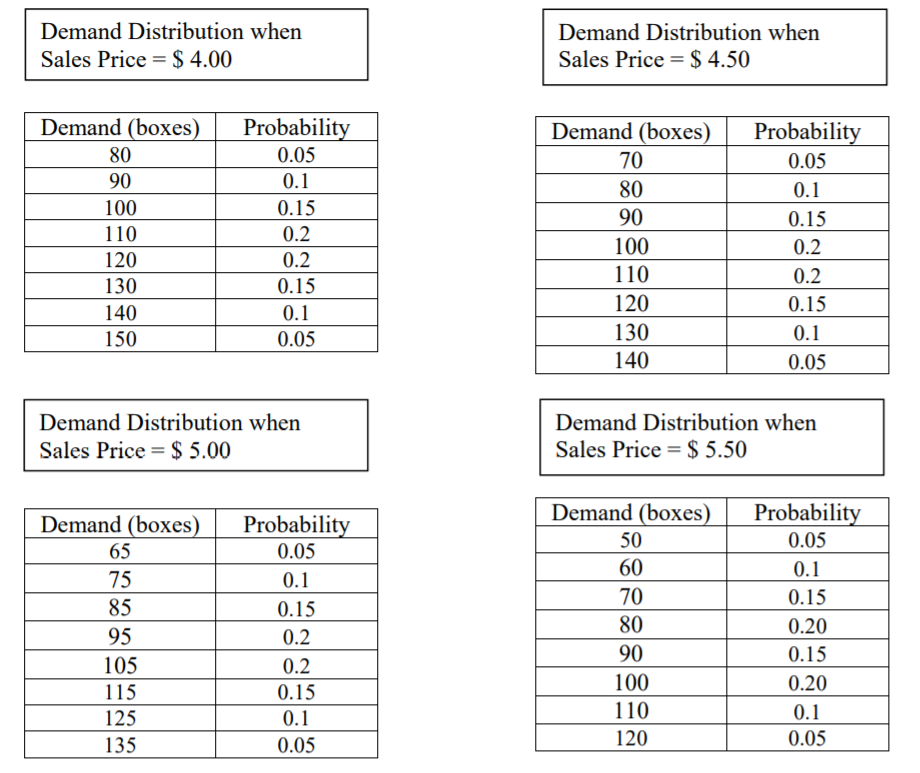
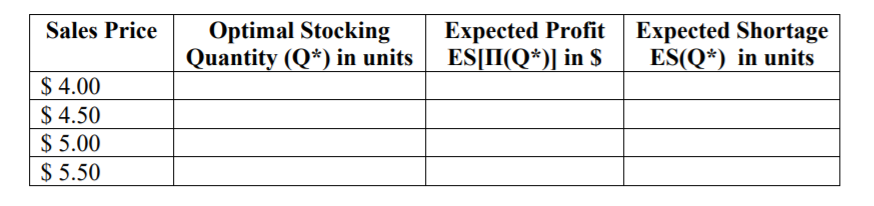
The Supermarket Store is about to place an order for Halloween candy. One best-selling brand of candy can be purchased at $ 2.50 per box before and up to Halloween. After Halloween, all the remaining candy can be marked down and sold for $ 1.00 per box. Assume that the loss in goodwill "cost" stemming from customers whose demand is not satisfied is $ 0.35. The store is considering a price per box of $ 4, $ 4.50, $ 5, and $ 5.50. Recognizing that demand is price dependent, through market research the store determines that demand distribution for these prices is as follows.

Demand Distribution when Demand Distribution when Sales Price = $ 4.00 Sales Price = $ 4.50 Demand (boxes) Probability Demand (boxes) Probability 80 0.05 70 90 0.05 0.1 80 100 0.15 0.1 110 0.2 90 0.15 120 0.2 100 0.2 130 0.15 110 0.2 140 0.1 120 0.15 150 0.05 130 0.1 140 0.05 Demand Distribution when Demand Distribution when Sales Price = $ 5.00 Sales Price = $ 5.50 Demand (boxes) Probability Demand (boxes) Probability 65 0.05 50 0.05 75 0.1 60 0.1 85 0.15 70 0.15 95 0.2 80 0.20 105 0.2 90 0.15 115 0.15 100 0.20 125 0.1 110 0.1 135 0.05 120 0.05Sales Price Optimal Stocking Expected Profit Expected Shortage Quantity (Q*) in units ES[HI(Q*)] in $ ES(Q*) in units $ 4.00 $ 4.50 $ 5.00 $ 5.50